ضریب بالستیک و تأثیر آن روی ساچمه
ضریب بالستیک و تأثیر آن روی ساچمه
BALLISTIC COEFFICIENT (BC)
پروفسور مایک رایت Mike Wright توضیحیاتی فنی دربارهی ضریب بالستیک و تأثیر آن روی ساچمه ارائه میدهد
گردآوری و ترجمه : میثم کماسایی
برای بسیاری از تیراندازان مفهوم «ضریب بالستیک» آشنا و در عین حال گیج کننده است. اغلب ما برای محاسبهی مسیر گلوله (trajectory)، انرژی و متغیرهای دیگر در بردهای مختلف، نرمافزارهایی را به کار میگیریم که از ضریب بالستیک ساچمهی مورد نظر استفاده میکنند. با این حال، چند نفر از ما واقعاً ماهیت ضریب بالستیک را درک میکنند؟ ضریب بالستیک یک ساچمه در اصل کمیتی است که نشان دهندهی مقاومت ساچمه در برابر نیروی درگ (drag) هوا و حفظ سرعت خود هنگام طی کردن مسافت است: هرچه این ضریب بزرگتر باشد، کاهش سرعت کمتر خواهد بود. مفاهیم اولیه دربارهی چگونگی اثرگذاری نیروی درگ بر سرعت ساچمه تقریباً واضحند. با این حال پیشینهی تحقیقات دربارهی بالستیک گلوله، که به خلق مفهوم ضریب بالستیک انجامید، آن را مقداری گیج کننده کرده است.
«ضریب بالستیک یک ساچمه در اصل کمیتی است که نشان دهندهی مقاومت ساچمه در برابر نیروی درگ هوا و حفظ سرعت خود هنگام طی مسیر میباشد»
در دههی 1860، یک کشیش بریتانیایی به نام فرانسیس بشفورث (Francis Bashforth) آزمایشاتی برای بررسی کاهش سرعت پرتابههای توپخانهای با استفاده از پاندول بالستیک انجام میداد. به سبب مشکلاتی که در اندازهگیری سرعتها در انتهای مسیر پرتابه برای گلولههای مختلف وجود داشت، بشفورث مفهوم «گلولهی استاندارد» را تعریف کرد که عملکرد بالستیک گلولههای دیگر با توجه به آن محاسبه میشد (با تغییر مقیاسها و بدون نیاز به انجام آزمایشات بیشتر). به این شکل او مفهوم ضریب بالستیک (یا به طور دقیقتر مفهوم معکوس آن، «ضریب درگ») را بر اساس یک پرتابهی استوانهای با 1 اینچ قطر و 1 پوند وزن را تعریف کرد. ضریب بالستیک این گلولهی استاندارد برابر 1.0 تعریف شد. ساچمههای تفنگ بادی ابعاد بسیار کمتری دارند و وزنشان 500/1 وزن گلولهی استاندارد است. بنابراین تعجبی ندارد که ضرایب بالستیک آنها بسیار کمتر از 1 باشد. مقدار این ضریب برای اکثر ساچمهها بین 0.01 تا 0.04 بسته به کالیبر، وزن و شکل ساچمه متغیر است. در عمل، ضریب بالستیک واقعی یک ساچمه هنگام پرواز، به الگوی ساخت لولهی تفنگ و مکانیزم قدرت رسانی؛ یعنی فنر یا PCP نیز بستگی دارد.
از جنبههای بسیاری وارد کردن مفهوم ضریب بالستیک – که توسط بسیاری از محققان بازتعریف شده است – به حوزهی تفنگ بادی ناخوشایند است؛ زیرا کار کردن با مفهوم واضحی مثل ضرایب درگ، همانطور که دیگر شاخههای علم مهندسی از آن استفاده میکنند، بسیار آسانتر است. با این حال، امروزه مفهوم ضریب بالستیک به خوبی جای خود را در تحقیقات و نرمافزارهای مربوط به بالستیک تفنگهای بادی باز کرده است و نیاز است که از معنای واقعی آن مطلع باشیم. بهترین راه برای درک این مفهوم، بررسی نحوهی اثرگذاری نیروی درگ هوا بر مسیر ساچمه است.
نیروی درگ هوا (Air Drag)
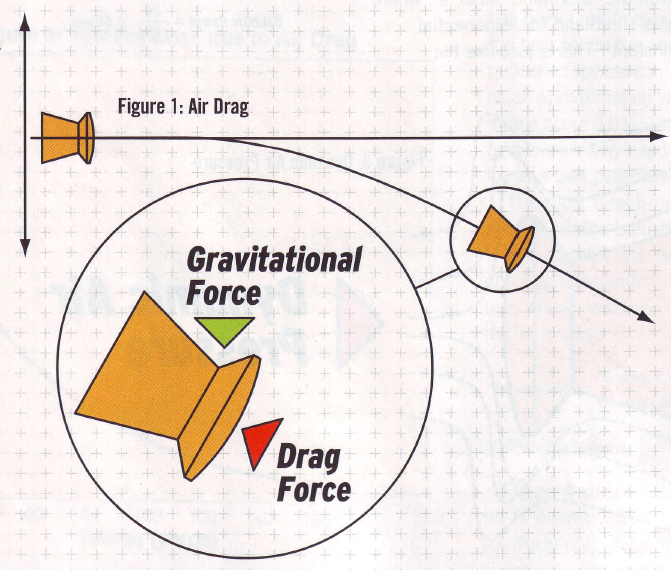
شکل 1 پرواز یک ساچمه را که از لولهای افقی شلیک شده نشان میدهد. با صرف نظر از اثر باد، ساچمه تحت اثر دو نیرو قرار دارد: یک نیروی ثابت عمودی ناشی از جاذبه و یک نیروی متغیر ناشی از درگ هوا. مجموع این نیروها باعث ایجاد خط سیر منحنی و رو به پایین نشان داده شده در شکل میشود.
برای فهم درست چگونگی ترکیب نیروهای جاذبه و درگ و تولید یک خط سیر مشخص، باید بفهمیم که چگونه درگ هوا در طول پرواز ساچمه تغییر میکند. با افزایش سرعت، نیروی درگ نیز افزایش مییابد که این به جریان هوا روی سطح ساچمه وابسته است. در ناحیهی زیر صوتی (subsonic)، که سرعت جریان هوا کمتر از عدد ماخ 1 (یعنی سرعتهایی تا حداکثر 950 فوت بر ثانیه) است و همهی ساچمههای تفنگهای بادی در این ناحیه هستند، نیروی درگ متناسب با مجذور سرعت ساچمه افزایش مییابد. از آنجا که کاهش شتاب ساچمه، یا «درگ هوا»، با این نیرو متناسب است، فرمول سادهی زیر صادق خواهد بود:

مقدار ثابت در این فرمول، یعنی میدان بالستیک ساچمه، ارتباط نزدیکی با ضریب بالستیک دارد. در تیراندازی واقعی، بیشتر تغییرات سرعت ساچمه نسبت به زمان برای ما جالب است تا تغییرات آن نسبت به زمان؛ بنابراین فرمول نیروی درگ را بهتر است بر آن مبنا تعریف کنیم:

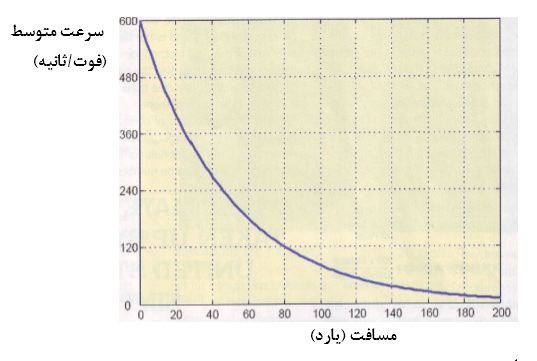
توجه داشته باشید که برای یک مسافت مشخص، درصد کاهش سرعت در اثر نیروی درگ هوا ثابت است. این نکتهای ضروری برای بقای سرعت و یک حقیقت کلیدی در تعریف منحنی سرعت – مسافت است. برای توضیح این نکته، بیایید نگاهی به مثالی از یک ساچمهی بسیار ضعیف بیندازیم. ساچمهای را در نظر بگیرید که سرعتش در دهانهی تفنگ 600 ft/sec و در یک میدان 10 یاردی مقدار آن به 492 ft/sec برسد؛ یعنی ساچمه 18% از سرعت خود را در یک میدان 10 یاردی از دست میدهد. در طی 10 یارد بعدی، 18% دیگر از سرعت کاسته شده و به مقدار 403 ft/sec میرسد. در مسافت 30 یاردی، نیز به همین شکل سرع به 337 ft/sec میرسد و با همین روند، ساچمه کل مسافت را طی میکند. شکل 2 نشان میدهد که نیروی درگ چگونه سرعت ساچمه را هنگام طی کردن مسیر میکاهد.
شکل 2: کاهش سرعت ناشی از درگ هوا
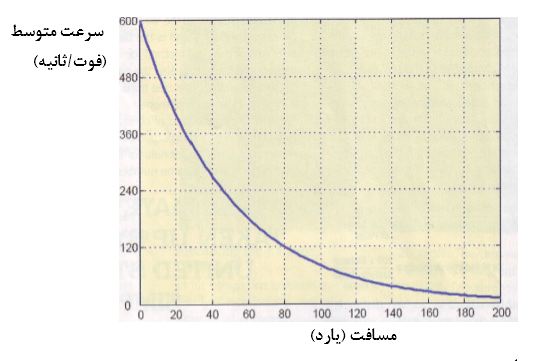
الگوی درصد کاهش ثابت در فواصل زمانی مساوی، پدیدههای زیادی را در دنیای اطراف ما کنترل میکند. برای مثال، تشعشعات رادیو اکتیو با همین الگو متلاشی میشوند، همچنین برای تخمین قدمت آثار قدیمی به روش کربن سنجی نیز از آن استفاده میشود. فواصل بین حلقهها در تنهی یک درخت نیز از این الگو پیروی میکند. برای نشان دادن میزان کاهش ارزش پول در یک بازهی ثابت تورم نیز از آن استفاده میشود. این الگو را منحنی کاهش نمایی (exponential decay) مینامند و فرمول آن، فارغ از زمینهی مورد استفاده، همواره دارای مقدار ثابتی است (2.7183 تا چهار رقم اعشار). معادلهی کاهش سرعت ساچمه نسبت به مسافت این گونه است:

به سبب این که عدد 2.1783 در همهی تحلیلهای دینامیکی مکرراً ظاهر میشود، آن را به اختصار با e نشان میدهند که مخفف (exponential constant) میباشد. این عدد نیز دقیقاً مثل 3.1416 است که به دلیل تکرار زیاد عدد پی نامیده میشود. با استفاده از e فرمول سرعت به این شکل در میآید:


این نتایج همگی خوبند، ولی ما باید قبل از هرگونه محاسبات برد بالستیک هر ساچمه را بدانیم. اگر فرمول سرعت را به شکل لگاریتمی بنویسیم، برد بالستیک را به این صورت میتوان محاسبه کرد:
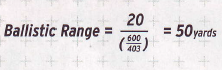
در اینجا ln لگاریتم طبیعی نسبت سرعت است. روی همهی ماشین حسابهای علمی دکمههای «ex» و «ln» وجود دارد. این توابع در بسیاری از نرمافزارهای (spread sheet) کامپیوتری هم موجودند.
بیایید ببینیم این فرمول چگونه در مورد مثال ما به کار میرود. ابتدا مقدار برد بالستیک (ballistic range) را محاسبه میکنیم. میدانیم که سرعت خروجی (muzzle) از 600 ft/sec به 403 ft/sec در فاصلهی 20 یاردی رسیده است، بنابراین برد بالستیک برابر است با:
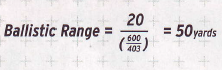
اکنون با استفاده از این مقدار میتوانیم سرعت را در یک فاصلهی دیگر بدست آوریم، مثلاً 35 یارد:
= سرعت در 35 یارد

این سرعت را میتوان در شکل 2 یافت و مشاهده کرد که با فاصلهی 35 یاردی متناظر است. فرمول برد بالستیک یک روش ساده در اختیار ما میگذارد تا دو سرعت اندازهگیری شده در دو فاصلهی متفاوت را برای اندازهگیری مقدار برد پرتابه استفاده نماییم. اما این ثابت، یعنی برد بالستیک چگونه با ضریب بالستیک مرتبط میشود؟
ضریب بالستیک و برد بالستیک
برای درک مفهوم امروزی و زجر آور ضریب بالستیک، بررسی پیشینهی آن کمک کننده خواهد بود. با این که مفهوم ضریب بالستیک به شکل امروزی آن، به عنوان معیاری برای راندمان پرواز گلوله، توسط بشفورث شکل گرفت، اولین بار پروفسور پیتر تیت که در کمبریج و ادینبرو کار میکرد فرمولی دقیق از پرتابهها که شامل مفهوم برد بالستیک نیز میشد، در دههی 1860 چاپ کرد. حدود 20 سال بعد، کمپانی کراپ (Krupp) در آلمان، اولین اندازهگیریهای دقیق را روی تأثیر درگ هوا بر مسیر حرکت گلوله در سال 1881 انجام داد. این کار با شلیک آزمایشی گلولههای ته صاف و نوک پهنی انجام شد که با طراحی استاندارد ساخته شده بودند.

پس از آزمایشات کراپ، مهندسان ارتش در روسیه (مایفسکی) و ایتالیا، روی استخراج یک مدل ریاضی برای محاسبهی خط سیر گلوله کار میکردند که ظاهراً خبر نداشتند پروفسور تیت پیش از آن مشکل را حل کرده بود (در آن زمان گوگل وجود نداشت!). مدل مایفسکی (Mayevski) متعاقباً توسط کلنل جیمز اینگالز (Ingalls) از ارتش ایالات متحده مورد استفاده قرار گرفت. او در صدد ساده سازی نتایج مایفسکی برای استفاده توسط پرسنلی بود که از ریاضیات آگاهی چندانی نداشتند. این انگالز بود که ضریب بالستیک را به شکلی توجیه کرد که معیاری از راندمان بالستیک هرگونه پرتابه، متناسب با گلولهی استاندارد باشد و این مفهوم را به شکل امروزی در آورد. این نتایج به صورتی که امروزه همچنان به عنوان «جداول اینگالز» شناخته میشوند به چاپ رسیدند.
«مدل مایفسکی متعاقباً توسط کلنل جیمز اینگالز از ارتش ایالات متحده مورد استفاده قرار گرفت. او در صدد ساده سازی نتایج مایفسکی برای استفاده توسط پرسنلی بود که از ریاضیات آگاهی چندانی نداشتند.»
ایدهی مقیاس بندی راندمان بالستیک یک گلولهی استاندارد برای تعیین عملکرد یک پرتابهی دلخواه دیگر (مثل ساچمهی تفنگ بادی)، نیاز به آن دارد که فیزیک مسأله تماماً در نظر گرفته شود. قبل از این یک مقالهی دقیق در این باره در مجلهی ورزش تفنگ بادی (Airgun Sport) منتشر کردهام که خلاصهی آن به این شرح است:
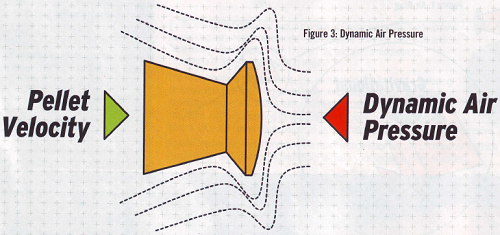
جریان هوا روی ساچمه، یک فشار دینامیکی هوا به وجود میآورد، که با مجذور سرعت ساچمه و چگالی هوا رابطه دارد. این موضوع در شکل زیر نشان داده شده است.
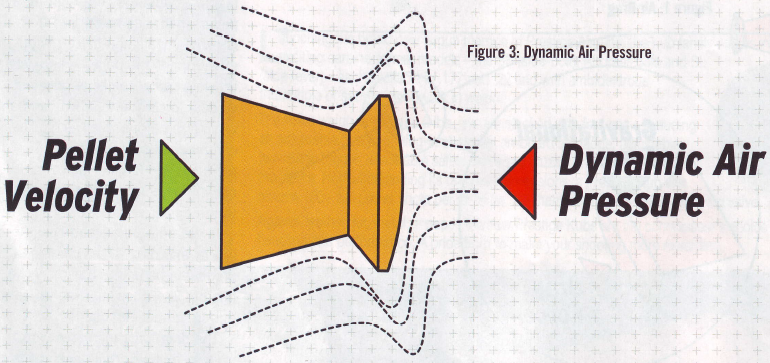
این فشار که توسط مساحت مؤثر جلوی ساچمه چند برابر میشود، نیروی درگ را روی ساچمه ایجاد میکند که اگر آن را بر جرم ساچمه تقسیم کنیم،کاهش سرعت ناشی از درگ هوا (deceleration air drag) را بدست میدهد؛

ضریب بالستیک را معمولاً به این صورت بدست میآورند:
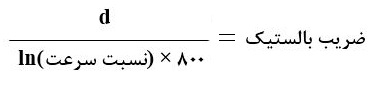
که همیشه در واحد پوند – اینچ محاسبه میشود. ضریب i را «ضریب شکل» ساچمه مینامند که نشان دهندهی مساحت مؤثر پیشانی و مقدار درگ است.
با استفاده از BC و مقایسه با فرمول محاسبهی درگ، آشکار است که ضریب بالستیک تنها یک نسخهی مقیاسی از برد بالستیک است. اگر واحدها را به درستی استفاده کنیم خواهیم داشت:
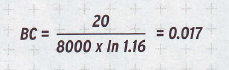
بنابراین برای ساچمهای که مثال زدیم، ضریب بالستیک برابر 0.0063 = 8000/50 است. بیایید نتایج کلیدی را تا اینجا خلاصه کنیم:
- در سرعتهای زیر صوتی، درگ هوا متناسب با مجذور سرعت ساچمه تغییر میکند.
- کاهش سرعت با افزایش مسافت به گونهایست که در هر بازهی افزایش مسافت، درصد کاهش سرعت ثابت است.
- منحنی سرعت بر حسب مسافت به صورت نزولی و نمایی است.
- نرخ کاهش بستگی به بالستیک رنج (BR) ساچمه دارد؛ هر چه BR بیشتر باشد، ساچمه بهتر سرعت خود را حفظ میکند.
- BR را میتوان با اندازهگیری سرعت ساچمه در دو نقطه محاسبه کرد.
- ضریب بالستیک برابر برد بالستیک بر حسب یارد تقسیم بر 8000 است.
اندازهگیری ضریب بالستیک
در مقالهی دیگری جیم تایلر تلاشها و فراز و نشیبهای اندازهگیری ضریب بالستیک را برای یک ساچمهی مشخص برمیشمارد. ممکن است فکر کنید که ارزش ندارد خود را درگیر این مشکلات کنیم، زیرا BC بسیاری از ساچمهها در اینترنت موجود است و با یک کلیک میتوان به آنها دسترسی داشت. اما شما در اشتباهید. ضریب بالستیک یک ساچمه به وزن و تلرانسهای ابعادی دقیق و همچنین شکل دقیق آن پس از شلیک بستگی دارد. بنابراین در بهترین حالت، اطلاعات منتشر شده را میتوان به عنوان تقریبی با 15% کمتر یا بیشتر در نظر گرفت. برای بدست آوردن مقادیر دقیق، باید خودتان این ضریب را برای تفنگ یا ساچمهایتان اندازهگیری کنید.
مستقیمترین روش برای اندازهگیری ضریب بالستیک، شلیک یک ساچمه روی دو کرونوگراف که در فاصلهی d از یکدیگرند میباشد، سپس از این فرمول استفاده میکنیم:
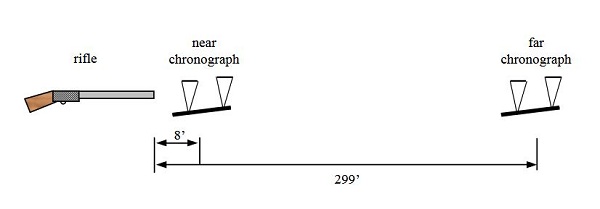

شکل 4 مجموعهای از منحنیها را نشان میدهد که عملیات ریاضی را برای سه فاصلهی 15، 20 و 25 یاردی کوتاه میکنند. استفاده از آنها بسیار آسان است. شکل 5 دیاگرامی از فرایند درگیر است. دو کرونوگراف در فاصلهی به دقت تعیین شدهای قرار داده شدهاند. d فاصلهی بین مراکز سنسورها میباشد. نزدیکترین زمانسنج (که در شکل با رنگ قرمز نشان داده شده است) سرعت V1 را میدهد. زمانسنج دورتر (سبز) نیز سرعت V2 را به ما میدهد. برای یافتن نسبت سرعت، V1 را بر V2 تقسیم میکنیم. فاصلهی d برابر 15، 20 یا 25 یارد است، بنابراین مقدار BC را میتوان از روی منحنی مربوطه خواند. برای مثال فرض کنیم V1 برابر 750 ft/sec و V2 برابر 647 ft/sec باشد. نسبت سرعت برابر 1.16 است. ضریب بالستیک (0.017) را میتوان مستقیماً از روی منحنی 20 یارد در شکل 4 خواند.
این مقاله، به همراه مقالهی جیم تایلر معرفی منطقیای از ضریب بالستیک ارائه میدهد و در مورد عدد کوچکی که در نرمافزارهای کامپیوتری وارد میکنیم توضیحاتی میدهد. با این حال، مقالهی جیم به ما میگوید که مسائل بیشتری هستند که باید روشن شوند.

