تأثیر شیارهای خان بر عملکرد گلوله ها

 

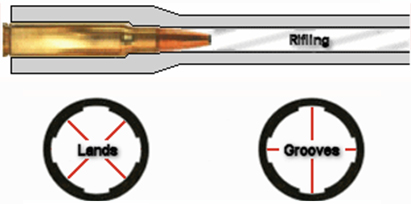
تأثیر شیارهای خان بر عملکرد گلوله ها

نویسنده : Sidra I. Silton و Paul Weinacht

     ایالت مریلند، شهر آبردین پروو گراوند، آزمایشگاه تحقیقات ارتش ایالات متحده  ۲۱۰۰۵-۵۰۶۶

چکیده

ما ترکیبی از تحقیق علمی و محاسباتی را در پیش گرفتیم تا تأثیر شیارهای خان را بر روی ویژگی های ایرودینامیکی پرتابه ها به دست بیاوریم و مشخص کنیم که آیا ویژگی های ایرودینامیکی مرتبط با شیارهای خان به صورت بالقوه مکانیسمی برای اصلاح زاویه های حین پرواز هستند یا خیر. این برنامه آزمایشی از شلیک پرتابه ها با استفاده از لوله های دارای توئیست استاندارد انجام می شد که دامنه سرعت آن در حدود سرعت پرواز پرتابه بود. علاوه بر این، گلوله ه های sabot-launched و pre- از لوله های بزرگ با نرخ چرخش خان بالا برای رسیدن به چرخش بیشتر گلوله شلیک میشد. روش محاسباتی برای اولین بار با استفاده از داده های موجود در تونل باد برای یک پرتابه تفنگ اعتبارسنجی شد. سپس نتایج محاسباتی برای تکمیل نتایج حاصل از آزمایش دامنه جرقه بدست آمد. نتایج نشان می دهد که اجزای ایرودینامیکی نسب به شیارهای تفنگ بیشتر حساس هستند و متاثر از نیروی مگنوس و roll-damping . این اثرات برای شرایط معمول در پرواز نسبتاً ناچیز هستند و اصلاح اثرات زاویه بعید به نظر می رسد و می توانند در تلاش های محاسباتی و تجربی آینده نادیده گرفته شوند.

• مقدمه

بسیاری از مهمات اسلحه به ثبات چرخش (Spin) نیاز دارند. شیارهای خان با ایجاد نرخ سرعت چرخش مطلوب در لوله این ثبات را ایجاد می کنند. برای مهمات کالیبر کوچک، شیارهای تفنگ بابدنه پرتابه درگیر می شوند. فرآیند  حکاکی توسط شیارهای تفنگ روی بدنه  پرتابه  هندسه  آن را قبل از پرتاب تغییر می دهد. گمان می رود که شیارهای خان می توانند بر ایرودینامیک  پرتابه  تأثیر بگذارند.

یکی از دلایل این که شیارهای ایجاد شده روی گلوله بر ایرودینامیک تأثیر می گذارند این است که  پرتابه  هنگام پرواز در مسافت های ابتدایی به حالت “چرخش بیش از حد” می رسد. هنگام شلیک از یک اسلحه ثابت، جریان نزدیک شیارها با شیارها برابر است در نتیجه باعث ایجاد ( قانون شرط مرزی – no-slip boundary condition) می شود (شکل ۱).

با حرکت پرتابه به سمت پایین، سرعت حرکت به سمت جلو از سرعت چرخش با سرعت بیشتری کاهش می یابد. این امر باعث می شود که جریان نزدیک شیارها با شیارها مطابقت نداشته باشد (شکل ۱) و باعث تولید حالت “بیش از حد چرخش – over-spun” می شود. شرایط بیش از حد چرخش ممکن است منجر به تغییر در مشخصات ایرودینامیکی  پرتابه  شود. 

بررسی صحیح تأثیر شیارهای پرتابی در هر دو برنامه آزمایشی و محاسباتی بعضی چالش ها را نشان میدهد و به طور کامل بررسی نمی شوند یا نادیده گرفته می شوند. دامنه آزمایشات برای تعیین ایرودینامیک یک  پرتابه به طور معمول در سرعت پایین آن با شارژ مهمات لازم و شلیک  توسط لوله “استاندارد” انجام می شود (McCoy, 1985; McCoy, 1990). اینها از دو طریق بر نتایج آزمایش تأثیر می گذارد. اول، سرعت spin در سرعت های شلیک شده با چرخش مربوطه در سرعت پرواز آزاد مطابقت ندارد. دوم،  پرتابه  ممکن است عمق حک شیار یکسانی نداشته باشد زیرا فشارهای داخل لوله ناشی از کاهش وزن باروت کاهش می یابد. از دیدگاه محاسباتی، افزودن شیارها یک ویژگی فیزیکی هندسی و جریان اضافی را ارائه می دهند که باید حل شود، بنابراین پیچیدگی و هزینه محاسباتی شبیه سازی افزایش می یابد. تاکنون، شبیه سازی های دینامیک سیالات محاسباتی ( (CFD یک مدل  پرتابه  بکر (غیر حکاکی) را در نظر گرفته اند (Sahu, 1986; Weinact et al., 1986). تلاش تحقیقاتی اخیر اثر شیارهای خان و چرخش بر ایرودینامیک مهمات کالیبر کوچک را به صورت آزمایشی و محاسباتی بررسی می کند. داده های موجود تونل باد، برای یک پرتابه شیاردار عمومی استفاده شد که رویکرد محاسباتی را تأیید می کند.. پس از آن، یک برنامه آزمایشی شلیک در یک مرکز spark-range aerodynamic برحسب محاسبات برای ارزیابی اثر شیارهای خان و چرخش بر روی پرتابه ایرودینامیکی اجرا شد.       

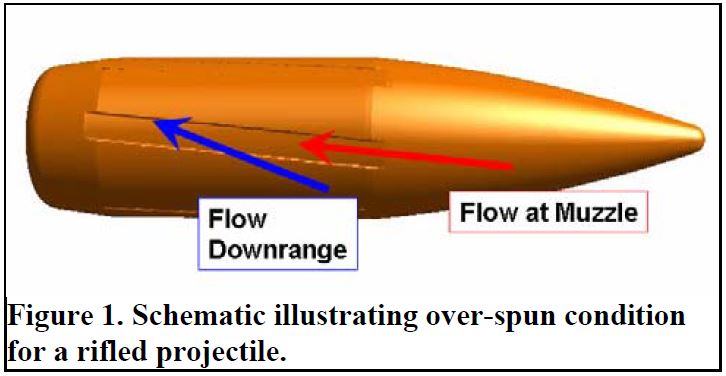
شکل ۱. نمودار توضیح شرایط چرخش بیش از حد برای یک پرتابه خان

 

• رویکرد محاسباتی

از روشهای محاسباتی برای بررسی تأثیر شیارهای پرتاب بر ایرودینامیک گلوله با استفاده از یک رویکرد شبکه بیش از اندازه تنظیم شده، استفاده کردیم (Renze و همکاران، ۱۹۹۲ ؛ Meakin، ۱۹۹۱) که از یک سیستم شبکه نزدیک بدنه و یک شکلک دکارتی خارج از بدنه استفاده می کند – مبتنی بر سیستم شبکه. سیستم شبکه نزدیک بدنه شامل شبکه های متصل به هم است که با قسمت های مختلف بدنه مطابقت دارد. سیستم شبکه دکارتی بیرونی و خارج از بدنه سیستم شبکه نزدیک بدنه را در بر می گیرد و تا مرز خارجی حوزه محاسباتی امتداد می یابد (شکل ۲). اتصال بین شبکه ای شبکه های نزدیک به بدنه و خارج از بدنه با هم تداخل دارند با استفاده از روش مشبک سازی بیش از حد Chimera ایجاد می شود (چان، ۲۰۰۲). سیستم شبکه نزدیک بدنه ۸۷٪ از ۵.۶ میلیون نقطه مورد استفاده برای شبکه کامل را شامل می شود.

حل معادلات قابل انعطاف ناوینر-استوکس با میانگین رینولدز با استفاده از کد ناسا، Overflow2 انجام شد. در محاسبات فعلی از یک طرح پیمایش زمان دقیق مرتبه اول سه عاملی مورب استفاده شده است که از تقسیم بندی دقیق مرتبه دوم در فضا استفاده می کند. مدل تلاطم تک معادله ای بالدوین-بارت (بالدوین و بارت، ۱۹۹۱را نیز به کار گرفتیم. خصوصیات را بر اساس شرایط مرز ورودی / خروجی در مرزهای دامنه اعمال کردیم. در سطح بدنه، شرایط مرزی بدون لغزش و آدیاباتیک را اعمال می کنیم.

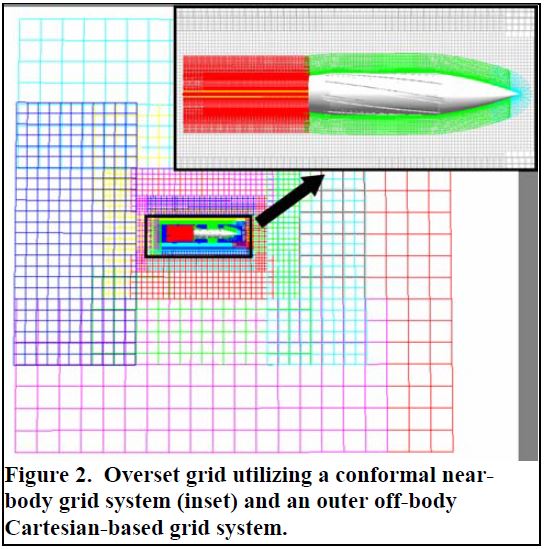
شکل ۲. شبکه بیش از حد تنظیم شده با استفاده از یک سیستم شبکه نزدیک بدنه مطابق (داخلی) و یک سیستم شبکه خارج از بدنه مبتنی بر دکارتی.

برای بدست آوردن ضرایب ایرودینامیکی استاتیک و همچنین میرایی رول (α = 0 درجه) و مگنوس (α = 2 درجه، ۵) یک سری محاسبات عددی با زاویه ثابت حمله، α و سرعت چرخش انجام می شود. درجه) متهمان چرخش و زاویه حمله ترکیبی برای بدنه های متقارن محوری را می توان با استفاده از یک حالت مرز سرعت مماس ساده روی سطح بدن، با یک رویکرد حالت پایدار برطرف کرد. با این حال، ترکیبی از چرخش غیر متقارن بدنه بدون محور و زاویه حمله، یک میدان جریان وابسته به زمان ایجاد می کند که نیاز به استفاده از یک رویکرد دقیق به زمان دارد. محاسبات وابسته به زمان با استفاده از یک شبکه نزدیک به بدنه ثابت و ثابت چرخش بدنه نسبت به سیستم شبکه دکارتی خارج از بدنه ثابت خارج از بدنه انجام شد. مشخص شد که تکرارهای درونی در هر مرحله زمان برای بدست آوردن یک محلول همگرا مناسب برای ضرایب ایرودینامیکی وابسته به چرخش مانند ضریب لحظه مگنوس و ضریب لحظه میرایی رول مورد نیاز است. برای هندسه صاف بدنه می توان نتایج دقیق زمان را با نتایج ثابت مقایسه کرد تا گام زمان مورد نیاز و تکرارهای داخلی تعیین شود. این مطالعه همچنین نشان داد که ۵۰۰۰-۷۰۰۰ مرحله زمانی فیزیکی، با ۲۰ تکرار داخلی برای به دست آوردن محلول چرخش حالت پایدار از محلول اولیه غیر چرخشی همگرا مورد نیاز است. این مربوط به زمان مورد نیاز برای یک ذره مایع برای حرکت یک تا دو طول بدنه در جریان آزاد است. مطالعات مربوط به اثر تکرارهای داخلی برای بدنه پرتابه شیاردار نیز انجام شد و نتایج مشابهی یافت شد.

برای بدست آوردن ضرایب میرایی گام در ارتباط با ایرودینامیک تولید شده با نرخ های زاویه ای غیر صفر، به مجموعه دوم آزمایشات عددی نیاز است. حداقل دو روش برای انجام آزمایش میرایی گام در حال حاضر وجود دارد که با تکیه بر حرکات تحمیل شده، نرخ های زاویه ای لازم برای تولید نیروها و لحظه های مرتبط با ضرایب میرایی زمین را تأمین می کنند. رویکرد ارائه شده در اینجا از یک حرکت مخروطی تحمیل شده برای تولید نیرو و گشتاور میرایی استفاده می کند، که می تواند مستقیماً از نیروی جانبی محاسبه شده و لحظه نرمال شده توسط زاویه حمله و سرعت مهار به دست آید (شیف، ۱۹۷۲ ؛ ویناخت، ۱۹۹۷ ؛ DeSpirito و همکاران، ۲۰۰۸). بسته به هندسه و نوع حرکت مخروطی انتخاب شده، این محاسبه را می توان به عنوان یک محاسبه حالت پایدار انجام داد.

داده های یکپارچه نیرو / لحظه جهانی با استفاده از ابزار FOMOCO از زمینه های جریان محاسبه شده بدست آمد (چان و بانینگ، ۱۹۹۶) توزیع نیرو و لحظه در امتداد بدنه نیز از طریق تغییرات جزئی در کد موجود و ابزار کمکی اضافی پس از پردازش، از زمینه های جریان محاسبه شده بدست می آید.

 

• رویکرد تجربی

اثر شیارهای خان در تاسیسات آزمایشگاهی ایرودینامیک ARL  را با روش تجربه بررسی کردیم. این مرکز برد جرقه برای ارزیابی کامل ایروبالیستیک گلوله ها طراحی شده است که براون آنرا تشریح کرده است (براون، ۱۹۵۸). مرکز برد شامل ۳۹ ایستگاه سایه افشان جرقه ای متعامد (شکل ۳) بیش از ۱۰۰ متر طول مسیر است که اولین ایستگاه تقریباً ۱.۸ متر پایین تر از پوزه قرار دارد. حسگرهای مادون قرمز عبور پرتابه از ایستگاه ها را تشخیص می دهند و یک سیستم کامپیوتری باعث ایجاد منابع جرقه ای می شود که یک تصویر سایه مستقیم عمودی و افقی از پرتابه عبوری روی فیلم ایجاد می کنند و زمان جرقه را ثبت می کنند. ایستگاه ها در یک سیستم امانتی بررسی می شوند که به طور همزمان با گلوله بر روی فیلم تصویربرداری می شود. فیلم پس از هر بار عکسبرداری و با استفاده از یک جدول نوری دقیق برای تولید داده های آزمایشی خام (دامنه، انحراف، ارتفاع، ارتفاع، زمین، خمیازه و رول) نسبت به سیستم مختصات محدوده ثابت زمین، به عنوان تابعی از زمان جرقه، خوانده می شود. با پردازش داده های خام با استفاده از تجزیه و تحلیل نظریه خطی استاندارد و یک روش تلفیقی عددی ۶-DOF در ARFDAS (ArrowTech Associates، ۱۹۹۷)، می توان مجموعه کاملی از ضرایب را بدست آورد.

شکل ۳. عکس ایستگاه های سایه افشان جرقه ای دو صفحه (متعامد) با محرک های حسگر مادون قرمز و منبع جرقه.

به منظور انجام تحقیقات آزمایشی در مورد تأثیر شیارهای خان و چرخش بر روی یک گلوله با کالیبر کوچک (به طور خاص ۵۶/۵ میلی متر)، از هر دو بمب دست نخورده و شیاردار استفاده شد (شکل ۴). با چرخش ثابت، پرتابه های شیاردار از یک بشکه M16A2 با استفاده از یک بار شارژ متغیر متغیر برای دستیابی به سرعت مطلوب شلیک می شوند. این شلیک ها نمایانگر روش معمولی است که برای توصیف ایرودینامیک گلوله های کالیبر کوچک استفاده می شود. برای به دست آوردن سرعت چرخش متناسب با سرعت پایین راندگی، دسته دوم پرتابه ها از بشکه M16A2 با استفاده از وزن استاندارد سوخت پیشرانه شلیک شده و از یک بلوک ژل در ۶۰۰ متر (از قبل حکاکی شده) بازیابی شدند. سپس پرتابه های از قبل حکاکی شده از پیچ های مناسب و با اندازه بیش از اندازه بشکه های Mann (7.62 میلی متر) خرابکاری شدند. اگرچه نماینده شرایط حین پرواز است، اما این روش به مراتب بیشتر از رویکرد معمول نیاز به تلاش دارد. پیکربندی سوم، متشکل از گلوله های بکری که از بشکه های بزرگتر به همان روش در پیکربندی دوم، خرابکاری شدند.

      

شکل ۴. گلوله های بکر (سمت چپ) و از قبل حک شده (راست) ۵.۵۶ میلی متر

4. نتایج

 

۱.۴ اعتبار سنجی عددی

 

اثر شیارهای خان و میزان چرخش با استفاده از نتایج حاصل از آزمایشات تونل باد موجود و آزمایش محدوده جرقه ایروبالیستی را ارزیابی کردیم. در هر حالت، نتایج تجربی با پیش بینی دینامیک سیالات محاسباتی افزایش یافت.

 

پیش بینی های محاسباتی برای اعتبارسنجی روش برای مدل تونل باد  را در شکل ۵ میتوان مشاهده کرد.  قطر مدل تونل باد ۵۱ میلی متر بود. اجازه آزمایش در تعداد رینولدز معادل یک گلوله ۲۰ میلی متری در شرایط جوی پرواز آزاد را می دهد. شیارهای تفنگ معادل آن برای تفنگ های ۲۰ میلی متری بود و شامل ۹ شیار، عرض ۱۱۱۱ کالیبر و عمق کالیبر ۰.۰۲۰۵ با سرعت چرخش ۱ چرخش در ۲۰ کالیبر سفر بود. آزمایشات تونل باد نیز در نسخه صاف (بدون شیار) مدل انجام شد. محاسبات در ۲.۰ ماخ برای یک عدد رینولدز بر اساس قطر ۹×۱۰۵ برای هر دو مدل صاف و شیاردار در طیف وسیعی از نرخ چرخش غیر بعدی از ۰ تا ۰.۴ انجام شد.

 

نیروها و گشتاورهای ایرودینامیکی برای هر دو مدل صاف و شیاردار را مقایسه کردیم. برای بسیاری از ضرایب ایرودینامیکی استاتیک، تأثیر کمی از شیارها مشاهده شد. برای ضریب درگ، اختلاف کمتر از ۰.۶٪ بود. برای ضرایب نیروی نرمال و لحظه فشار، اختلاف به ترتیب کمتر از ۱.۰٪ و ۲.۵٪ بود. هر دو پیش بینی و نتایج تونل باد در هنگام حضور شیارها، کاهش جزئی در لحظه انعطاف پذیری را نشان می دهد. برای بدنه شیاردار، پیش بینی ها نشان دهنده کاهش جزئی (۲٪) در لحظه انعطاف پذیری است زیرا نرخ چرخش غیر بعدی از ۰ به ۰.۴ افزایش یافته است. لحظه های پیچیده پیش بینی شده برای بدنه شیاردار در حدود٪ ۱٪ ضریب لحظه انعطاف پذیری منفرد گزارش شده از آزمون تونل باد بود. اختلافات معنی دارتری برای نیروی مگنوس (طرف) و لحظه و لحظه میرایی رول مشاهده شد.

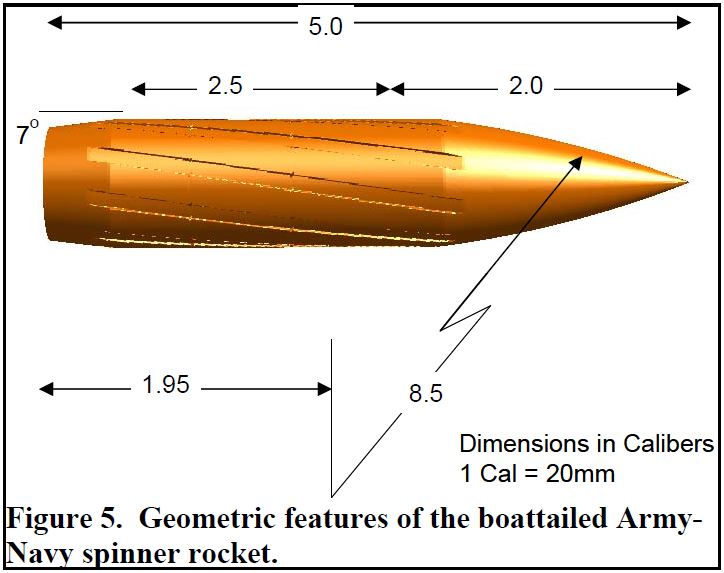
شکل ۵. ویژگی های هندسی پرتابه نظامی- دریایی.

لحظه رول و نیرو و لحظه مگنوس برای گلوله شیاردار تغییرات خطی کلاسیک را با مشخصه سرعت چرخش گلوله های صاف به نمایش می گذارد، به جز اینکه گلوله شیاردار به دلیل غیر متقارن بودن ماهیت، نیروی یا لحظه غیر صفر را با سرعت چرخش صفر به نمایش می گذارد. شیارهای خان بیشتر شبیه سازی های مسیر و روش های کاهش داده هیچ جبران چرخشی صفر را در این ضرایب فرض نمی کنند. بنابراین، یک روش برای به دست آوردن گشتاور میرایی رول و نیرو و گشتاور مگنوس، عادی سازی نیرو یا گشتاور با سرعت چرخش برای بدست آوردن یک ضریب “موثر” است که به نرخ چرخش وابسته است. از آنجا که سرعت چرخش در پرواز نسبتاً آهسته تغییر می کند و می تواند مستقیماً با شماره محلی ماخ مرتبط باشد، مگنوس “م ”ثر” اگرچه به چرخش وابسته است، اما می تواند به عنوان تابعی از تعداد ماخ رفتار شود.

 

تطابق کافی بین اندازه گیری های محاسبه شده و تونل باد از لحظه مگنوس موثر در شکل ۶ نشان داده شده است. تفاوت های نسبتاً کوچک بین مگنس مگنوس محاسبه شده در ۲.۲ و ۴.۳ درجه نشان می دهد که ضریب گشتاور مگنوس نسبتاً مستقل از زاویه پرتاب است (در حداقل برای زوایای کوچک) و می تواند به عنوان یک ثابت برای سرعت چرخش ثابت نشان داده شود. نتایج وابستگی لحظه مگنوس به نرخ چرخش، به ویژه برای نرخ چرخش کم را نشان می دهد. با سرعت چرخش بالاتر، با کاهش اثر جبران چرخش صفر، گشتاور مگنوس نسبتاً ثابت می شود. همانطور که قبلاً ذکر شد، سرعت چرخش غیر بعدی به طور معمول در طول پرواز افزایش می یابد زیرا سرعت جلو پرتابه سریعتر از سرعت چرخش بعدی کاهش می یابد. افزایش نرخ چرخش غیر بعدی فراتر از سرعت چرخش غیر بعدی ۰.۳۱۴ دیده می شود که به دلیل شیارها تغییرات نسبتاً کوچکی در گشتاور مگنوس (و پایداری دینامیکی) ایجاد می کند.

 

شکل ۷ ضریب میراگر رول موثر را برای بدنه ANSR در زاویه حمله ۲.۲ و ۴.۳ درجه نشان می دهد. در سرعت چرخش پرتاب (۰.۳۱۴)، میرایی رول موثر برای بدنه شیاردار تقریباً ۲۵٪ بیشتر از بدنه صاف است. میله میله موثر شیار شیار نسبت به بدنه صاف با چرخش بیش از حد گلوله افزایش می یابد. برای شرایط تحت چرخش، تغییرات بسیار بزرگتری در میرایی رول موثر امکان پذیر است، اگرچه این برای شرایط معمول پرتاب غیر منتظره است.

 

۴.۲ مهمات نسل ۵.۵۶ میلی متر

برای محاسبه تأثیر شیارهای خان بر روی مهمات نسل ۵.۵۶ میلی متری که به طور معمول از تفنگ M16A2 شلیک می شود، از روش محاسباتی معتبر و آزمایش دامنه جرقه استفاده شد. سه پیکربندی از پرتابه M193 (شکل ۸) برای این بخش از مطالعه در نظر گرفته شده است. بدنه شیاردار (از قبل حکاکی شده) با سرعت پیچشی ثابت مربوط به pD / V = ​​۰.۲ و در پرواز pD / V و بدنه صاف در pD / V در پرواز. آزمون های جرقه در دامنه های ۲.۶، ۲.۱، ۱.۶ و ۱.۱ در طی یک زاویه از حمله برای بدست آوردن مجموعه کاملی از ضرایب استاتیک و مشتقات دینامیک انجام شد. محاسبات برای ۲.۵ و ۱.۳۵ ماخ در دو درجه زاویه حمله در شرایط جوی استاندارد به پایان رسید. تفنگ در هندسه محاسباتی به عنوان شش شیار با عرض ۱۸/۰ کالیبر و عمق کالیبر ۰.۰۱ با سرعت پیچش بشکه M16A2 مدل سازی شده است. شبیه سازی های اضافی CFD در مدل بدنه صاف در محدوده بزرگتر از تعداد Mach برای مقایسه بیشتر با نتایج تجربی تکمیل شد.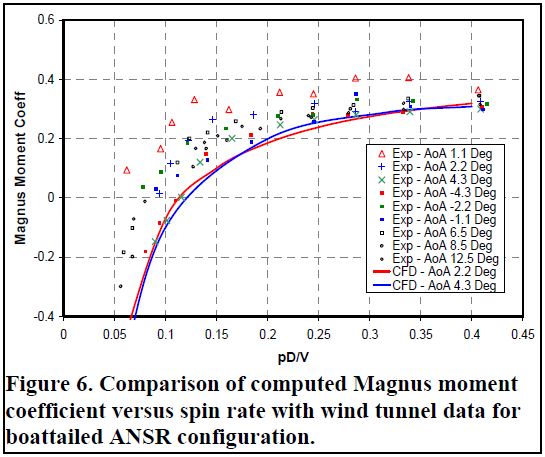

شکل ۶. مقایسه ضریب گشتاور مگنوس محاسبه شده در برابر سرعت چرخش با داده های تونل باد برای پیکربندی ANSR قایقرانی.

 

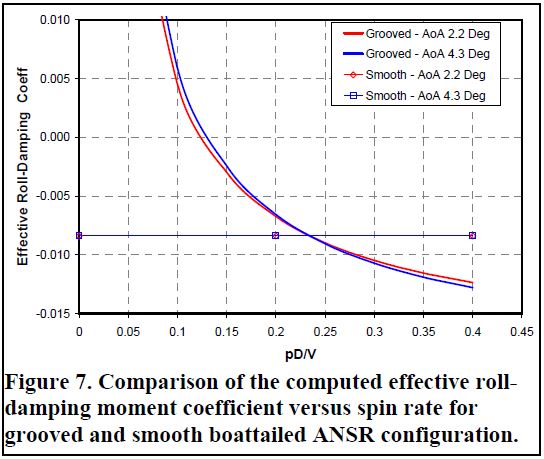
شکل ۷. مقایسه ضریب گشتاور موثر میرایی میله رول در برابر سرعت چرخش برای پیکربندی ANSR شیاردار و صاف

 

شکل ۸. ویژگی های هندسی ۵.۵۶ میلی متر M193.

مشابه مدل تونل باد، تفاوت بسیار کمی در بیشتر ضرایب ایرودینامیکی بین تنظیمات دیده می شود که نشان می دهد نه سرعت چرخش و نه حکاکی تأثیر مهمی برای نتایج تجربی یا محاسباتی، به ویژه ضرایب استاتیکی ندارد. شکل ۹ پیش بینی ضریب نیروی محوری صفر-خمیازه را نشان می دهد. داده های محدوده تفاوت معناداری بین تنظیمات قابل توجه نشان نمی دهد. توافق با نتایج محاسباتی کاملاً خوب است. توجه داشته باشید که در حالی که محاسبات مگنوس در α = 0 درجه انجام شد، محاسبات مخروطی در α = 2 درجه به پایان رسید. اختلاف ۱-۲٪ مربوط به کشش درجه دوم خمیازه است. ضرایب نیروی طبیعی و گشتاور فشار در شکلهای ۱۰ و ۱۱ نشان داده شده است. در حالی که فقط نتایج مدل محاسباتی بدنه صاف نشان داده شده است، تمام داده های دامنه

 

مشمول. توافق بین تنظیمات دامنه و همچنین محاسبه های مخروطی (نرخ چرخش صفر) و مگنوس (نرخ زاویه ای صفر) عدم حساسیت هر دو این ضرایب به چرخش و سرعت زاویه ای را نشان می دهد. باز هم، مهمترین تفاوتها دوباره در لحظه مگنوس و لحظه میرایی رول مشاهده شد.

 

مشتقات دینامیکی در کنار گذاشتن اثرات حکاکی نرخ چرخش کاملاً رو به جلو نبودند. به نظر می رسد اثر هر یک بر ضریب گشتاور میرایی زمین کم باشد (شکل ۱۲). مقایسه دامنه جرقه و اندازه گیری های محاسبه شده ضریب گشتاور مگنوس موثر در شکل ۱۲ نشان داده شده است. مقدار زیادی از پراکندگی در داده های تجربی وجود دارد، اما با سرعت چرخش یا حکاکی ارتباط ندارد. این در دقت اندازه گیری دامنه است که می تواند به اندازه ۲۵-۳۰ باشد. نتایج محاسباتی در این دقت روند داده های آزمایشی را به خوبی دنبال می کنند.

 

مقایسه دامنه جرقه و اندازه گیری محاسبه شده ضریب گشتاور مگنوس موثر در شکل ۱۳ نشان داده شده است. نتایج دامنه جرقه دارای مقدار زیادی خطای آزمایشی است، به ویژه با نزدیک شدن ضریب گشتاور مگنوس به صفر. اگرچه داده های دامنه و نتایج محاسباتی کاملاً منطبق نیستند، اما روندها قطعاً مشابه هستند. در نزدیک سرعت پرتاب، داده های دامنه و محاسبات هیچ تفاوتی را نشان نمی دهند، انتظار می رود که جریان با شیارها همسو باشد. با کاهش سرعت، داده های دامنه جرقه نشان می دهد که پرتابه پیچ تاب دارای مقادیر ضریب کمتری نسبت به دو پیکربندی دیگر است. در کمترین تعداد Mach، محاسبات و داده های دامنه هر دو نشان می دهد که پرتابه شیاردار با pD / V در پرواز دارای ضریب لحظه مگنوس کمی بالاتر است. اختلافات مشاهده شده در این کمترین تعداد ماخ با توجه به بیشترین چرخش پرتابه بسیار ناچیز است. در حقیقت، تفاوت بین پیکربندی ها در نتایج آزمایشی به سختی خارج از خطای اندازه گیری است. بنابراین، تغییرات در نتایج محاسباتی نیز به ویژه قابل توجه مشاهده نمی شوند.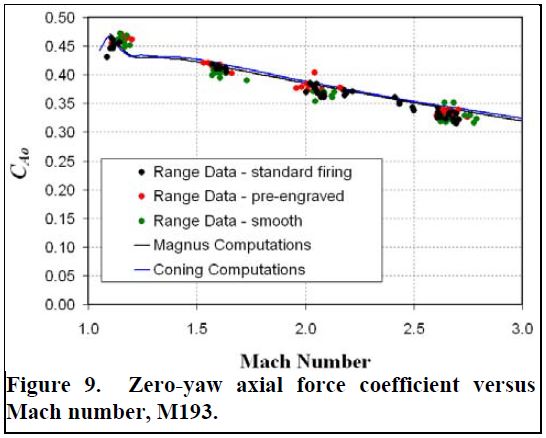

 

شکل ۹. ضریب نیروی محوری صفر-خمیازه در مقابل تعداد Mach، M193.

 

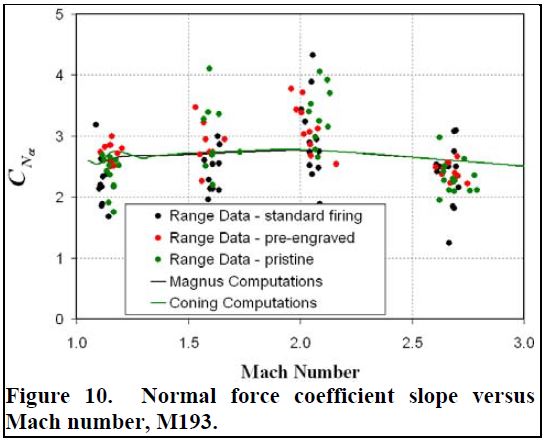
شکل ۱۰. شیب ضریب نیروی عادی در برابر تعداد Mach، M193.

 

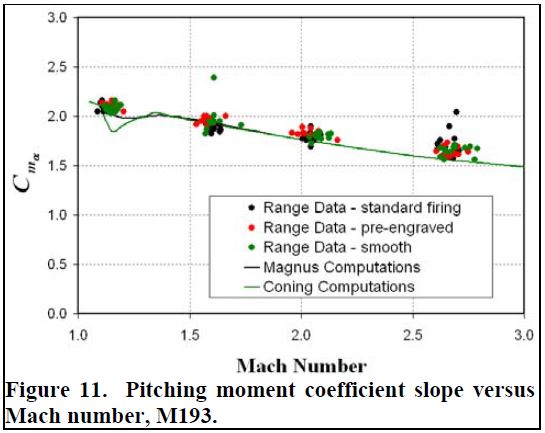
شکل ۱۱. شیب ضریب لحظه پیچش در برابر تعداد Mach، M193.

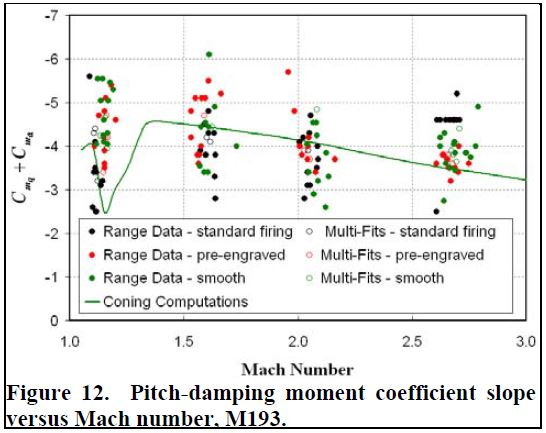
شکل ۱۲. شیب ضریب گشتاور میرایی در برابر تعداد Mach، M193.

 

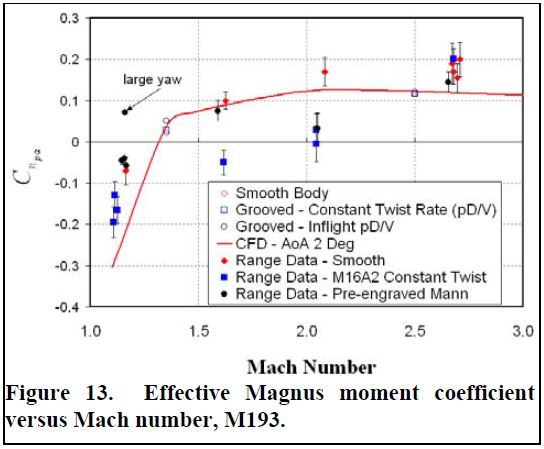
شکل ۱۳. ضریب گشتاور مگنوس موثر در برابر تعداد Mach، M193.

 

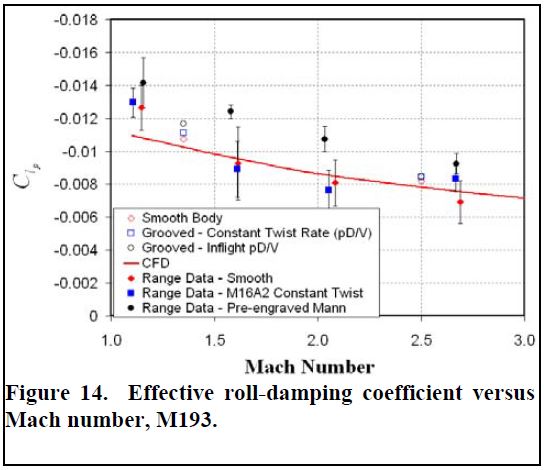
شکل ۱۴. ضریب میرایی رول موثر در برابر تعداد Mach، M193.

شکل ۱۴ ضریب میرایی رول موثر برای تصاویر متغیر M193 بررسی شده را نشان می دهد. میله های خطا در داده های دامنه جرقه نشان دهنده یک انحراف استاندارد از میانگین ضریب میرایی رول است. در سرعت پرتاب (نزدیک) داده های دامنه و نتایج محاسباتی ضریب میرایی رول را برای پیکربندی بدنه صاف کمی پایین تر نشان می دهد. در خطای آزمایش بالستیک، تغییرات قابل توجه نیستند. در دو عدد ماخ پایین تر، داده های دامنه نشان می دهد که پرتابه از قبل حک شده در پرواز pD / V دارای ضریب موثر میرایی رول قابل اندازه گیری بزرگتر است. با این حال، در کمترین تعداد Mach، اختلافات دوباره در خطای داده های تجربی است. نتایج محاسباتی تأیید می کند که بدنه شیاردار در pD / V در پرواز دارای یک ضریب میرایی رول کمی بالاتر در تعداد ماخ پایین است، اما این به دلیل تغییر داده های تجربی قابل توجه نیست.

 

۴.۳ پایداری دینامیکی و زاویه اصلاح

 

با استفاده از خصوصیات ایرودینامیکی (محاسباتی یا آزمایشی) که به عنوان بخشی از این مطالعه تکمیل شده است، می توان برای هر پیکربندی پایداری، عملکرد و مسیر حرکت ۶ درجه آزادی پرتابه را ارزیابی کرد. از آنجا که ضرایب ایرودینامیکی به طور قابل توجهی بین تنظیمات متفاوت نبود، مسیر دور تحت تأثیر پیکربندی آزمایش شده قرار نمی گیرد. با این حال، هر دو ثبات و عملکرد، با توجه به زاویه اصلاح می توانند تحت تأثیر پیکربندی انتخاب شده قرار بگیرند. به طور خاص، یک نرخ پیچش ثابت یا سرعت چرخش پرواز به عنوان ثبات دور به سرعت چرخش بستگی دارد.

 

برای اینکه یک پرتابه با چرخش ثابت بتواند یک پرواز پایدار داشته باشد، دور باید از نظر ژیروسکوپی و پویا در طول مسیر پرواز پایدار بماند. برای اینکه یک دور از نظر ژیروسکوپی پایدار باشد، فاکتور پایداری ژیروسکوپی، Sg، داده شده توسط معادله (۱) باید بزرگتر از یک باشد.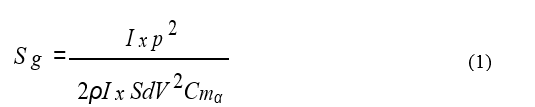

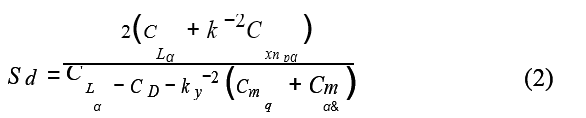
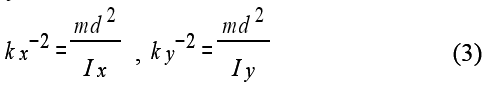
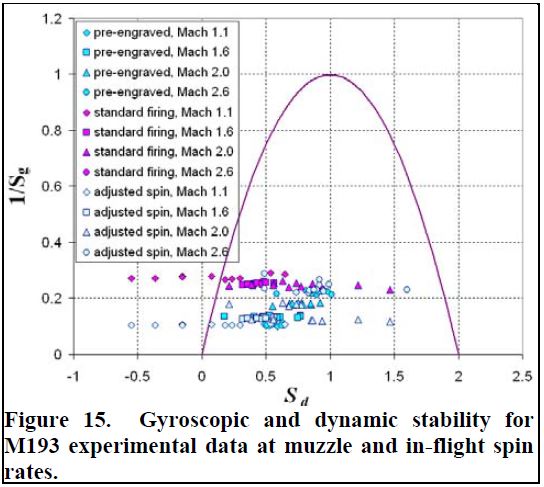
با فرض ژیروسکوپی بودن دور، می توان ثبات پویای دور را ارزیابی کرد. عامل پایداری دینامیکی، Sd توسط داده می شود

جایی که ρ تراکم جریان آزاد است، d قطر پرتابه است، S منطقه مرجع پرتابه است، V سرعت جریان آزاد است و Ix لحظه محوری اینرسی است. علاوه بر این،

جایی که m جرم پرتابه است و آن لحظه عرضی اینرسی است. توجه داشته باشید که تمام ضرایب ایرودینامیکی در معادلات (۱) و (۲) در ضرب می شوند

علاوه بر این، پرتابه باید در ثبات پویایی محدود شده توسط تعریف شده باقی بماند

شکل ۱۵ نمودار معکوس عامل پایداری ژیروسکوپی را در مقابل پایداری دینامیکی برای تنظیمات استاندارد شلیک (pd / V ثابت) و از قبل حکاکی شده (pd / V در پرواز) با پایداری دینامیکی محدود، S1 = S نشان می دهد d (2 – S d)، روکش شده است.

شکل ۱۵. ثبات ژیروسکوپی و پویا برای داده های تجربی M193 با سرعت چرخش پوزه و در پرواز.

 

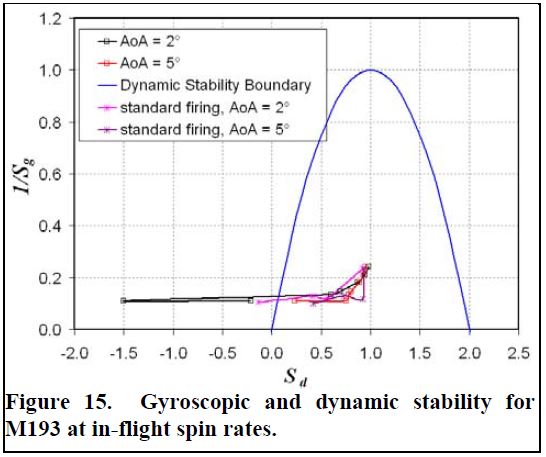
شکل ۱۵. ثبات ژیروسکوپی و دینامیکی M193 با نرخ چرخش در پرواز.

همچنین در شکل ۱۵ پیکربندی شلیک استاندارد برای pd / V در پرواز تنظیم شده است. داده های دامنه نشان می دهد که پرتابه از نظر ژیروسکوپی در تمام سرعت ها پایدار است. همانطور که انتظار می رفت، گرمهای دورهای قبل از حکاکی و دورهای چرخش تنظیم شده با شلیک استاندارد دارای Sg بزرگتر به دلیل سرعت چرخش بیشتر مطابقت دارند. پرتابه همچنین برای اعداد ماخ بیشتر از ۱.۵ ماخ به صورت پویا پایدار است. به نظر می رسد در نزدیکی Mach 1.1، پایداری دینامیک دور به نوع پیکربندی و همچنین زاویه حمله بستگی دارد. پایداری دینامیکی دورهای پیش حکاکی شده به طور قابل توجهی افزایش یافته و تمام دورهای پیش حکاکی شده در ماخ ۱.۱ پایدار هستند. بی ثباتی دینامیکی نشان می دهد که ممکن است یک چرخه محدود کوچک خمیازه رخ دهد. در واقع یک چرخه محدود کننده خمیازه کوچک برای پیکربندی شلیک استاندارد Mach 1.1 (تقریباً ۲ درجه) وجود داشت. افزایش پایداری دینامیکی دورهای قبل از حکاکی به دلیل این پیکربندی دارای ضریب گشتاور مگنوس بزرگتر (کمتر منفی) نسبت به پیکربندی شلیک استاندارد است. این را می توان تا حدی به دور قبل از حکاکی دارای سطح خمیازه بالاتر (۱.۵ درجه <α <8 درجه) نسبت به دور شلیک استاندارد (۰.۳ درجه <α <4 درجه) نسبت داد. با این حال، بر اساس پایداری شلیک استاندارد چرخش، انتظار می رود کمترین دورهای قبل از حکاکی ناپایدار باشد. عکسهای کم خمیازه اضافی (زیر ۲ درجه) از پیکربندی از قبل حکاکی شده برای تعیین دقیق تر چرخه محدود لازم است.

 

فاکتورهای پایداری نیز برای بدنه صاف محاسباتی از ۱.۱ تا ۳ ماخ با سرعت چرخش پرواز محاسبه شده اند (ضرایب با pd / V ثابت تعیین می شوند). پیش بینی ها نشان می دهد که پرتابه از نظر ژیروسکوپی پایدار است (sg> 1) در تمام سرعت ها. مقایسه این نتایج با نتایج استاندارد شلیک، چرخش تنظیم شده، نشان می دهد که شیارهای تفنگ حداقل تأثیر دارند. همانند پرتابه منقوش، پرتابه صاف در رژیم عددی ماخ پایدار باقی می ماند مگر در نزدیکی ۱.۱ و ۱.۲ ماخ در زاویه کم حمله که نشان دهنده یک چرخه محدود کوچک خم است. توافق بین نتایج بدنه صاف محاسباتی و نتایج استاندارد شلیک آزمایشی، اعتماد نویسندگان را برای استفاده از هر یک از این دو روش در آینده افزایش می دهد.

 

نتیجه گیری ها

یک روش محاسباتی پیچیده برای بررسی تأثیر تفنگ و سرعت چرخش بر روی مشخصات ایرودینامیکی مهمات کالیبر کوچک استفاده شده است. رویکرد محاسباتی با مقایسه با داده های تونل باد برای یک هندسه گلوله اصلی با شیارهای خان در Mach تأیید شده است

 

محاسبات نشان می دهد که اثر نسبی بین پرتابه های صاف و شیاردار (مچ دار) در محدوده ای از سرعت چرخش حداقل است و شیارهای خان اثرات ایرودینامیکی مسئول زاویه های اصلاح شده تولید نمی کنند. سپس این روش به یک گلوله های کالیبر کوچک نسل فعلی. در رابطه با یک آزمایش دامنه جرقه، اثر شیارهای خان و سرعت چرخش (پیچ و تاب ثابت در برابر پرواز pD / V) در سرعت راه اندازی و کاهش سرعت بر روی ضرایب ایرودینامیکی و مشتقات به حداقل رسیدند یا در خطای آزمایشی تست بالستیک.

 

نتایج پیامدهای مهمی برای هر دو آزمایش CFD و آزمایش هوازی از مهمات کالیبر کوچک دارد. به مقدار فوق العاده ای از منابع محاسباتی و تجربی اضافی برای به دست آوردن یک پرتابه با حکاکی مناسب با سرعت چرخش مورد نیاز بود که مربوط به تعداد ماخ مورد بررسی باشد. خوشبختانه، نتایج فعلی نشان می دهد که تأثیر شیارهای خان و میزان چرخش برای تعیین ضرایب ایرودینامیکی و مشتقات دینامیک اهمیت خاصی ندارد، بنابراین می توان از روشهای CFD و تجربی استفاده کرد. با این حال، اگر بخواهیم ثبات دور را برای سرعت های پایین به درستی تعیین کنیم، استفاده از سرعت چرخش در پرواز ضروری است. اگر فقط از نرخ چرخش پوزه استفاده شود، سطح پیش بینی شده بی ثباتی دینامیکی، که به صورت زاویه اصلاح ظاهر می شود، احتمالاً بیشتر از واقعیت خواهد بود.

 

تشکر و قدردانی

نویسنده لازم میداند از PM-MAS ارتش ایالات متحده برای تأمین اعتبار و حمایت از بخشهای قابل توجهی از این تلاش قدردانی کند. این کار همچنین با اعطای وقت رایانه از مرکز دفاع عمده منابع مشترک وزارت دفاع در آزمایشگاه تحقیقات ارتش ایالات متحده پشتیبانی می شود.

 

منابع

Arrow Tech Associates, “ARFDAS: Ballistic Range Data Analysis System,” User and Technical Manual, South Burlington, VT, May 1997.

Baldwin, B.S. and Barth, T.J., “A One-Equation Turbulence Transport Model for High Reynolds Number Wall-Bounded Flows,” AIAA-91-610, January 1991.

Braun, W.F., “The Free Flight Aerodynamics Range,” BRL-R-1048, U.S. Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD, July 1958.

Chan, W.M., “The Overgrid Interface for Computational Simulations on Overset Grids,” AIAA-2002-3188, June 2002.

Chan, W.M. and Buning, P.G., “User’s Manual for FOMOCO Utilities – Force and Moment Computation Tools for Overset Grids,” NASA-TM-110408, July 1996.

DeSpirito, J., Silton, S.I., and Weinacht, P., “Navier-Stokes Predictions of Dynamic Stability Derivatives: Evaluation of Steady State Methods,” AIAA-2008-0214, Jan. 2008.

McCoy, R.L., “Aerodynamic Characteristics of Caliber

.۲۲ Long Rifle MATCH Ammunition, BRL-MR-3877, Ballistic Research Laboratories, Aberdeen Proving Ground, MD, Nov 1990.

McCoy, R.L., “Aerodynamic and Flight Dynamic Characteristics of the NEW Family of 5.56MM NATO Ammunition,” BRL-MR-3476, Ballistic Research Laboratories, Aberdeen Proving Ground, MD, Oct 1985.

Meakin, R.L., “A New Method for Establishing Inter-grid Communication Among Systems of Overset Grids”, AIAA Paper AIAA-91-1586, June 1991.

Renze, K.J, Buning, P.G., and Ragagopalan, R.G., “A Comparative Study of Turbulence Models for Overset Grids”, AIAA Paper AIAA-92-0437, January 1992.

Sahu, J.,”Three Dimensional Base Flow Calculation for a Projectile at Transonic Velocity,” AIAA-86-1051, May 1986.

Shiff, L.B., “Nonlinear Aerodynamics of Bodies in Coning Motion,” AIAA Journal, Vol. 10, No. 11, 1972, pp. 1517 – ۱۵۲۲.

Weinacht, P., “Navier-Stokes Predictions of Pitch Damping for Axisymmetric Projectiles,” J. of Spacecraft and Rocket, Vol. 34, No. 6, 1997, pp. 753-761.

Weinacht, P., Guidos, B.J., Sturek, W.B., and Hodes, B.A., “PNS Computations for Spinning Shell at Moderate Angles of Attack and for Long L/D Finned Projectiles,” BRL-MR-3522, Ballistic Research Laboratories, Aberdeen Proving Ground, MD, June 1986.