تجزیه و تحلیل آیرودینامیکی و دینامیکی سه ساچمه رایج با کالیبر ۴.۵ mm در یک جریان ترنسونیک

ساچمه‌های بررسی شده دارای کالیبر مشابه ۴.۵ mm هستند، اما شکل دماغه یا هد متفاوتی دارند. این ساچمه‌ها دارای تقارن محوری هستند و شامل سه نوع اصلی سرتخت، نوک تیز، و سرگِرد می‌شوند. بعد از اینکه این ساچمه‌ها از نظر هندسی مدل‌سازی شدند، معادلات ناویر استوکس به عنوان معادلات حاکم بر میدان جریان اطراف ساچمه‌ها حل شدند. نتایج آیرودینامیک محاسبه شده به منظور تحلیل مسیر پرتابه‌ها از نظر دینامیکی استفاده شدند. تغییر ضریب درگ به وسیله عدد ماخ جریان آزاد (که نکته کلیدی برای تحلیل دینامیکی حرکت پرتابه است) به دست آمد. تحلیل دینامیکی حرکت پرتابه‌ها به طور دقیق مسیر را توصیف می‌کند و توضیح می‌دهد چطور سرعت ساچمه و ارتفاع با زمان و مکان کاهش می‌یابند. با اتکا به این تحلیل‌ها،از نقطه نظر آیرودینامیکی و دینامیکی، ساچمه سرگرد در یک محدوده از اعداد ماخ بهترین رفتار‌های آیرودینامیکی و دینامیکی را در مقایسه با ساچمه‌های دیگر نشان می‌دهد.

واژه‌های کلیدی: ناویر استوکس، معادلات، روش جیمسون، جریان ترنسونیک، تحلیل دینامیکی.

۱- مقدمه

یکی از عملی‌ترین موضوعات در آیرودینامیک، تحلیل حرکت یک پرتابه است، که به وسیله محاسبه چندین پارامتر آیرودینامیکی و دینامیکی انجام می‌شود. بعد از تحلیل یک پرتابه واکنشی M864 مجهز به سیستم دمش پایه با استفاده از محاسبات ناویر استوکس در سال ۱۹۹۵، نیتوبیز و گیبلینگ[۱] تأثیر نیروی رانشی روی بردار‌های سرعت را در ناحیه ویک با اعداد ماخ کمتر از ۱ تا حدود ۳ بررسی کردند، و در نهایت مسیر موشک را به درستی پیش‌بینی کردند [۱]. سیلتون[۲] به منظور پیش‌بینی تأثیر چرخش روی جریان سیال از محاسبات ناویر استوکس برای پرتابه چرخان از سرعت‌های زیرصوتی تا فراصوتی در زوایای حمله مختلف استفاده کرد [۲]. ساهو[۳] دینامیک سیالات محاسباتی (CFD) را با دینامیک اجسام صلب (RBD) ترکیب کرد و توانست مسیر چندین پرتابه و موشک را با و بدون حرکات چرخشی در شرایط ناپایا به طور موفقیت آمیز شبیه‌سازی کند [۳]. وایناخت[۴] که قبلاً معادلات ناویر استوکس را برای پیشبیینی‌های دمپینگ پیچ[۵] پرتابه‌های با تقارن محوری حل کرده بود [۴]، برای نشان دادن تأثیر خان‌های مارپیچ روی عملکرد مهمات با کالیبر کوچک با سیلتونین[۶] همکاری کرد [۵]. آن‌ها سپس در یک کار عددی-آزمایشی با استفاده از یک تونل باد با دی‌سپیریتو[۷] همکاری کردند که منجر به توضیح این مسئله شد که چطور نیرو‌ها و تکانه‌های ناشی از چرخاندن پرتابه روی پایداری دینامیکی آن تأثیر می‌گذارند [۶]. چند سال بعد، ساهو یک مطالعه محاسباتی انجام شده برای محاسبه آیرودینامیکی‌های پرواز آزاد یک پرتابه چرخان در رژیم سرعت از سرعت‌های زیرصوتی تا فراصوتی را با استفاده از یک تکنیک CFD/RBD ترکیبی پیشرفته توصیف کرد. در قسمت CFD این کار از یک تکنیک محاسباتی ناویر استوکس استفاده شد. روش CFD/RBD ترکیبی امکان شبیه‌سازی‌های پرواز مجازی با زمان دقیق پرتابه‌ها را فراهم کرد و به طور همزمان آیرودینامیک و دینامیک‌های پرواز را به شکلی یکپارچه پیش‌بینی کرد [۷]. سپس ساهو و هیوی از تکنیک‌های CFD حالت پایا و CFD/RBD ترکیبی برای محاسبه آیرودینامیک‌های مرتبط با پرواز آزاد پرتابه باله‌دار هم با فلپ‌های[۸] کوچک و هم بدون فلپ‌های کوچک استفاده کردند. محاسبات ناویر استوکس انجام شدند و حل‌های حالت پایا از سرعت‌های زیرصوتی تا فراصوتی به دست آمدند. نتایج محاسبه شده از کار آن‌ها نشان داد که فلپ‌های کوچک در سرعت‌های تراصوتی بی‌اثر بودند و در سرعت‌های فراصوتی مؤثر بودند [۸]. آمیتش کومار[۹] و همکاران ، جریان اطراف یک دماغه مخروطی را با یک پرتابه دُم گِرد برای رژیم‌های جریان زیرصوتی، تراصوتی و فراصوتی به صورت عددی بررسی کردند. مشاهده شد تا زمانی که نیروی درگ مد نظر است پرتابه دم گرد نسبت به پرتابه دم قایقی گزینه بهتری است [۹].

در این مقاله، تحلیل آیرودینامیکی و دینامیکی سه ساچمه رایج تفنگ‌های بادی که قبلاً به صورت عددی گزارش نشده است انجام شد. پرتابه‌های مورد نظر به ترتیب دارای سه نوع اصلی ساچمه سرتخت، نوک تیز، و سرگرد هستند. برای انجام این کار، بعد از شبیه‌سازی هندسه ساچمه‌ها، معادلات ناویر استوکس به عنوان معادلات حاکم بر میدان جریان اطراف ساچمه‌ها است حل شدند. تأثیر هندسه ساچمه‌ها روی پارامتر‌هایی از قبیل درگ و فشار بررسی شد. علاوه بر این، از نتایج به دست آمده در حل عددی یک سیستم معادلات دیفرانسیل معمولی به عنوان معادلات دینامیک حاکم بر حرکت پرتابه استفاده شد. بدین طریق، مسیر و سرعت ساچمه‌ها پیش‌بینی شدند.

۲- شبیه‌سازی هندسه ساچمه‌ها

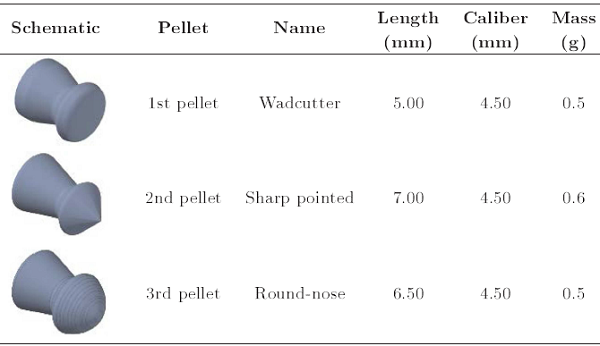
اولین مرحله تحلیل، شبیه‌سازی هندسه ساچمه‌ها است. در اینجا فرایند شبیه‌سازی با کمک یک دوربین دیجیتال انجام شد. با استفاده از حالت عکاسی سوپرماکروی[۱۰] دوربین چند عکس دقیق گرفته شد. به منظور افزایش کیفیت عکس‌ها، عکس‌برداری در یک محیط روشن انجام شد (شکل ۱). بعد از آن، هندسه ساچمه‌ها به دقت با خطوط و منحنی‌ها منطبق شد، که در شکل ۲ نشان داده شده است. سپس تمام مختصات لازم که هندسه ساچمه‌ها را مشخص می‌کنند به کمک یک نرم‌افزار استخراج شد. در نهایت، ابعاد ساچمه‌ها به وسیله یک کولیس با دقت ±۰.۰۱ mm اندازه‌گیری شد و برای پی بردن به چگالی ساچمه‌ها، آن‌ها به وسیله یک ترازوی دیجیتال با دقت ±۰.۱ g وزن شدند (جدول ۱). نمودار حاصل از ساچمه‌ها در شکل ۳ نشان داده شده است.

شکل ۱: ساچمه کالیبر ۴.۵ mm: (a) سرتخت؛ (b) نوک تیز؛ و (c) سرگرد.

شکل ۲: انطباق منحنی‌ها با هندسه (a) اولین ساچمه، (b) دومین ساچمه، و (c) سومین ساچمه.

۳- مش‌بندی (شبکه‌بندی) دامنه

یکی از رایج‌ترین روش‌های تولید شبکه، روش بیضی است. در این روش، هم مرز فیزیکی بدنه ساچمه و هم مرز خارجی که ساچمه را در بر می‌گیرد باید تعریف شوند.

مرز خارجی ناحیه‌ای را مشخص می‌کند که در آن جریان سیال باید حل شود. این دامنه همانطور که در اینجا نشان داده شده است، به صورت یک ناحیه دایر‌ه‌ای اطراف بدنه با یک شعاع ۱۵ بار بزرگتر از شعاع غیر واقعی پرتابه که شامل ۳۷۷ در ۶۰ نقطه شبکه است تعریف می‌شود. از آنجایی که جریان سیال ویسکوز است، برای نشان دادن تأثیر دقیق لایه مرزی، سلول‌هایی که به بدنه نزدیک هستند بیشتر فشرده شد‌ه‌اند. شبکه تولید شده در دامنه راه‌حل برای اولین ساچمه در شکل ۴ نشان داده شده است.

جدول ۱: اندازه‌گیری فیزیکی ساچمه‌ها.

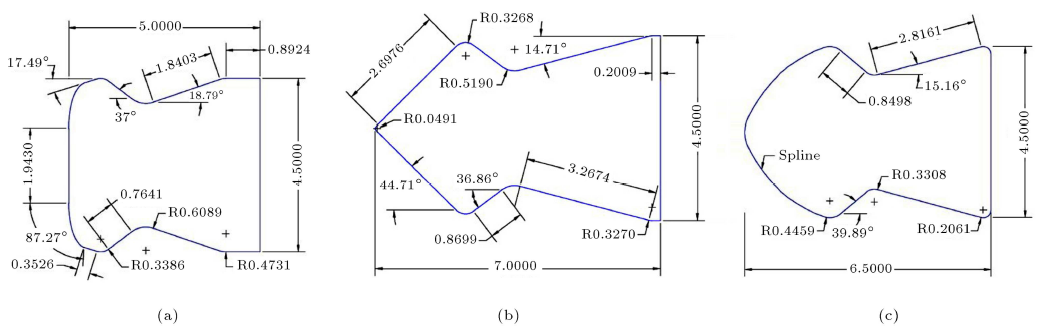
شکل ۳: نمودار (a) اولین ساچمه، (b) دومین ساچمه، و (c) سومین ساچمه.

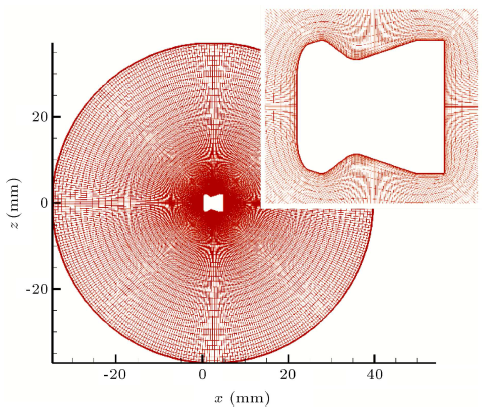
شکل ۴: مش‌بندی دامنه راه‌حل.

۴- معادلات آیرودینامیکی حاکم

به منظور تحلیل ساچمه‌ها از نظر آیرودینامیکی، معادلات ناویر استوکس تراکم‌پذیر دو بُعدی با تقارن محوری در یک دستگاه مختصات استوانه‌ای (x, r, θ) با استفاده از روش صریح جیمسون از نظر عددی حل شدند. این طرح از تفاضل مرکزی استفاده می‌کند که دارای دقت مرتبه دوم در فضا است [۱۰-۱۲]. معادلات حاکم بر جریان سیال را می‌توان به صورت زیر نوشت:

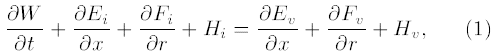
W یک متغیر وابسته است، Ei و Fi بردار‌های شار همرفتی هستند، و Hi نشان دهنده منبع لزج است؛ این متغیرها به صورت زیر تعریف می‌شوند:

به علاوه، Ev و Fv بردار‌های شار ویسکوز هستند، و Hv نشان دهنده منبع ویسکوز است که به صورت زیر به دست می‌آیند:

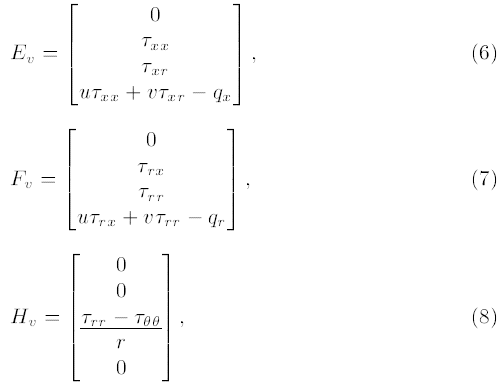
که در آن ρ و P به ترتیب چگالی و فشار بدون بُعد محلی هستند. τxx، τrr و τθθ تنش‌های نرمال هستند؛ τxr و τrx تنش‌های برشی هستند؛ و e مجموع انرژی داخلی و جنبشی برای واحد جرم سیال است که می‌تواند از رابطه زیر به دست آید:

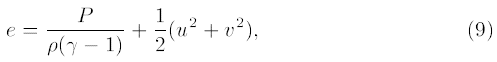
که در آن γ = Cp/Cv است. در اینجا جملات Cp و Cv ثابت‌های حرارت مخصوص به ترتیب برای فرایند‌های فشار ثابت و حجم ثابت هستند. به علاوه، تنش‌های نرمال و برشی بدون بُعد به صورت زیر هستند:

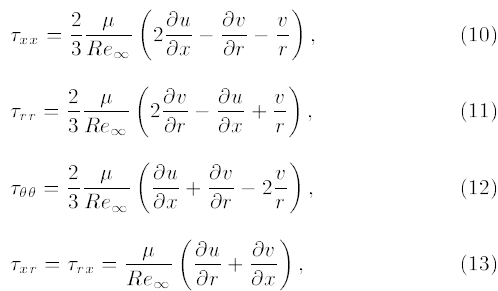
که در آن Re∞ عدد رینولدز جریان آزاد است که به صورت زیر تعریف می‌شود:

M∞ عدد ماخ جریان آزاد است، C سرعت صوت است، و D قطر ساچمه است که مساوی با کالیبرش است. μ ویسکوزیته دینامیک جریان محیط است که با فرض گاز اید‌ه‌آل برای هوای اطراف می‌تواند با استفاده از فرمول سوترلند ارزیابی شود [۱۳]. علاوه بر این، شار‌های حرارتی بدون بُعد در معادلات (۴) تا (۶) و (۴) تا (۷) به صورت زیر تعریف می‌شوند:

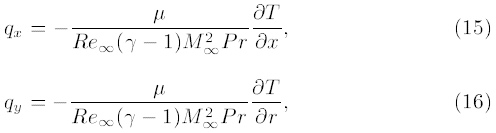
که در آن Pr عدد پرانتل است و T دمای بدون بُعد محلی است. پارامتر T می‌تواند به صورت زیر بیان شود:

معادلات آیرودینامیکی پایای حاکم، صرف نظر از رژیم جریان، همیشه هذلولی هستند. بنابراین، به منظور به دست آوردن حل حالت پایا برای هر عدد ماخ پرواز به عنوان شرط مرزی ورودی از تکنیک زمان پیمایشی جیمسون در محاسبات استفاده شده است؛ با شروع از توزیع‌های جریان اولیه حدسی، از معادلات پایا در زمان انتگرال گرفته شد تا زمانی که حل از زمان مستقل شود و بتواند به عنوان حل حالت پایا در نظر گرفته شود. در نتیجه، نرخ میانگین تغییر سراسری باقیمانده چگالی در کل دامنه محاسبه به عنوان معیار همگرایی حل عددی استفاده شد. این یک معیار رایج در دینامیک سیالات محاسباتی است و به صورت زیر تعریف می‌شود:

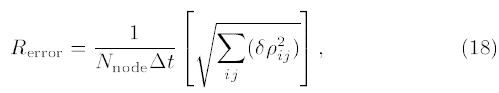
که در آن Nnode تعداد کل گره‌ها است، و δρ تغییر در چگالی در دو مرحله متوالی است. هنگامی‌ که Rerror < 0.01% است می‌توان این محاسبه را همگرا در نظر گرفت [۱۰،۱۴،۱۵]. با استفاده از یک سیستم با مشخصات Intel(R) CoreTM 2 Due CPU 2.53 GHz، زمان سپری شده برای حل معادلات ناویر استوکس برای یک عدد ماخ خاص حدود پنج دقیقه است.

۵- معادلات دینامیک حاکم

معادلات دینامیک حاکم به منظور به دست آوردن مسیر ساچمه‌ها بررسی شدند. این معادلات با استفاده از قانون دوم نیوتن در امتداد جهات عمود بر مسیر حرکت و مماس با مسیر حرکت به دست آمدند. نمودار حرکت جنبشی ساچمه در شکل ۵ نشان داده شده است.

بردار موقعیت پرتابه می‌تواند به صورت زیر نوشته شود:

که در آن x و z به ترتیب مؤلفه‌های افقی و عمودی بردار موقعیت هستند. همچنین، î و k̂ بردار‌های یکه در امتداد جهات x و z هستند. با گرفتن دو مشتق متوالی از ، بردار‌های سرعت و شتاب به صورت زیر به دست می‌آیند:

شکل ۵: نمودار حرکت جنبشی پرتابه

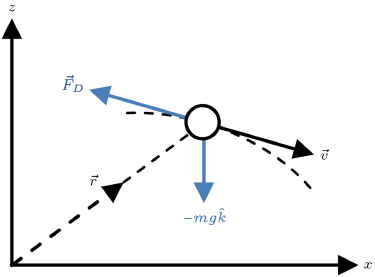
به علاوه، نیروی درگ  با سرعت پرتابه متناسب است، اما در جهت مخالف حرکت. بنابراین، نیروی درگ می‌تواند به صورت زیر نوشته شود:

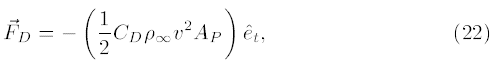
که در آن CD ضریب درگ است، ρ∞ چگالی جریان آزاد است، v بزرگی بردار سرعت  است، AP مساحت پلتفرم پرتابه است، و  بردار واحد مماس است. با استفاده از قانون دوم نیوتن داریم:

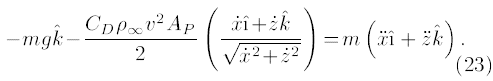
در نتیجه:

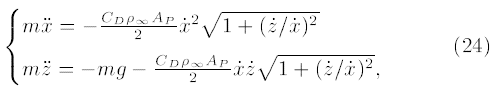
که در آن m جرم پرتابه و g شتاب گرانشی است. جمله (ż/ẋ)۲ دارای یک مقدار بی‌نهایت کوچک است و در نتیجه قابل چشم‌پوشی است. شرایط اولیه زیر برای سیستم معادلات دیفرانسیلی بالا فرض می‌شوند:

که در آن v0 سرعت اولیه ساچمه تفنگ بادی است.

در این مقاله، سیستم معادلات دیفرانسیلی (معادلات (۵) و (۶) با استفاده از روش رانگ-کوتای مرتبه چهارم حل شدند [۱۶]. همانطور که واضح است، سیستم معادلات شامل ضریب درگ CD است که خودش یک تابع از عدد ماخ است. یک جدول از مقادیر CD در مقابل M∞ به وسیله حل معادلات آیرودینامیکی حاکم در اعداد ماخ مختلف ارائه شده است. در نتیجه، تحلیل دینامیکی حرکت ساچمه در هر گام زمانی اساساً به نتایج آیرودینامیکی بستگی دارد؛ با این وجود، از آنجای که ضریب درگ CD = CD(M∞) به صورت یک تابع صریح در دسترس نیست، استفاده از یک روش درون‌یابی (مانند رگرسیون خطی) بین مقادیر CD موجود از جدول CD – M∞ فوق‌الذکر اجتناب‌ناپذیر است.

۶- اعتبارسنجی راه‌حل عددی

قبل از رفتن به مرحله بعد، راه‌حل عددی باید بررسی شود. بنابراین، جریان سیال روی یک پرتابه خاص با استفاده از روش جیمسون حل شد و نتایج به دست آمده با نتایج عددی مربوط به کار‌های پسندیده‌فرد و سرینیواس [۱۷] و داده‌های آزمایشی گزارش شده توسط لین و چییِنگ مقایسه شدند [۱۸]. مقایسه نتایج در شکل ۶ نشان داده شده است. همانطور که به وضوح می‌توان مشاهده کرد، توافق خوبی بین حل عددی و داده‌های آزمایشی وجود دارد.

شکل ۶: اعتبارسنجی راه‌حل عددی

 

۷- نتایج آیرودینامیک و بحث‌ها

در این بخش، حل‌های عددی معادلات ناویر استوکس توضیح داده می‌شود، که شامل تحلیل خطوط جریان، ضرایب درگ و فشار همراه با کانتور‌های فشار و ماخ می‌شود.

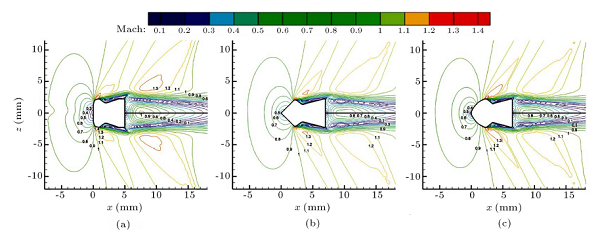
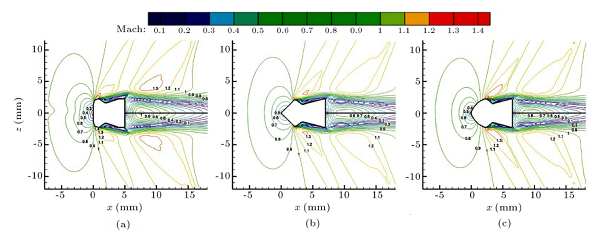
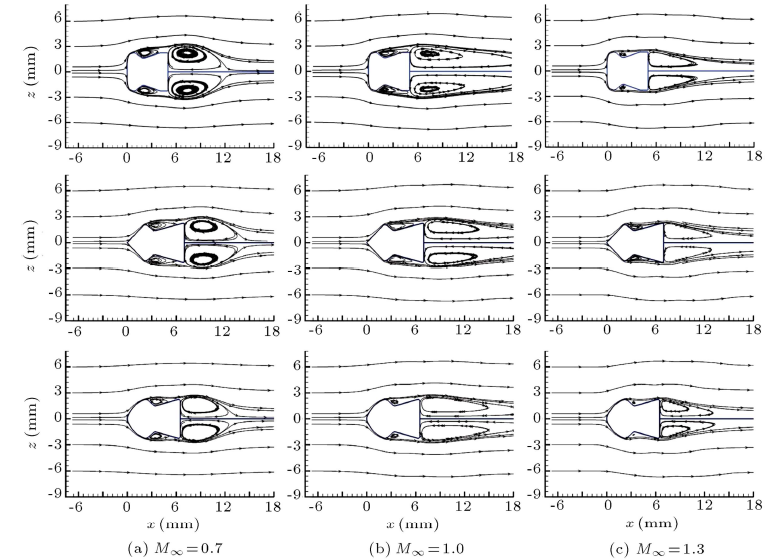
خطوط جریان میدان جریان روی تمام ساچمه‌ها در اعداد ماخ مختلف (M < 1, M = 1, M > 1) در شکل ۷ نشان داده شده است. ناحیه ویک که در جریان پایین دست سمت راست پشت ساچمه‌ها تولید می‌شود، یک ناحیه با فشار پایین است. از آنجایی که در یک عدد ماخ خاص، ناحیه ویک اولین، دومین و سومین ساچمه کوچکتر می‌شود، این پرتابه‌ها در طول پروازشان در یک جریان تراصوتی در معرض یک نیروی درگ فشاری کوچکتر هستند. از طرف دیگر، همانطور که می‌توان از شکل نتیجه‌گیری کرد، با افزایش عدد ماخ، ناحیه ویک یک ساچمه خاص کاهش می‌یابد؛ با این وجود، بررسی پارامتر‌های جریان سیال نشان می‌دهند که هرچه اعداد ماخ بیشتر باشند، مقادیر فشار در ناحیه ویک کمتر هستند. بنابراین، نیروی درگ فشاری با افزایش عدد ماخ افزایش می‌یابد، زیرا میدان جراین اختلافات فشار بیشتری را بین جریان بالا دستی و پایین دستی در اعداد ماخ بالاتر تجربه می‌کند.

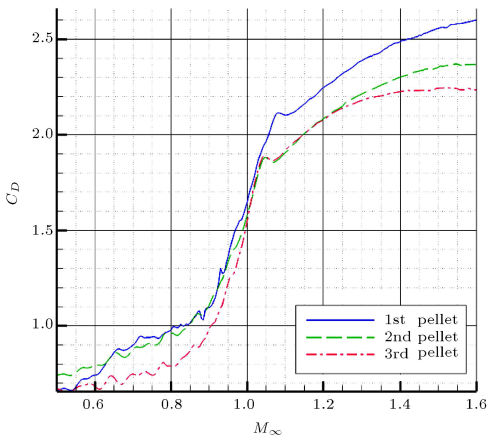
ضریب درگ CD در مقابل عدد ماخ در شکل ۸ نشان داده شده است. نظر به اینکه نیروی درگ که روی ساچمه عمل می‌کند به صورت حاصلضرب فشار دینامیک و ضریب درگ تعریف می‌شود، نمودار CD آنچه که قبلاً از تحلیل اثر کاهش ناحیه ویک روی ساچمه‌ها نتیجه گرفته شد را تأیید می‌کند.

شکل ۷: خطوط جریان در (a) M∞ = 0.۷، (b) M∞ = 1.۰، و (c) M∞ = 1.۳.

شکل ۸: ضریب درگ CD در مقابل عدد ماخ

ضریب فشار به صورت زیر تعریف می‌شود:

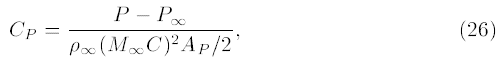
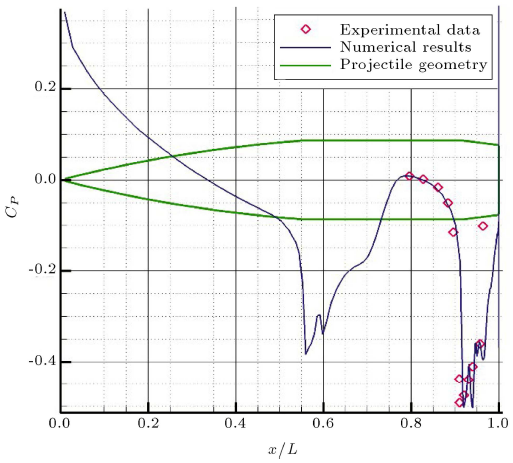
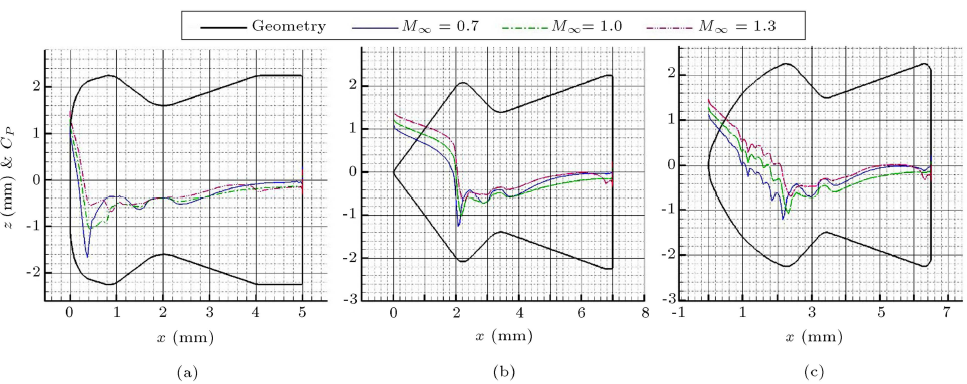
که در آن P و P∞ به ترتیب فشار اتمسفری و محلی هستند. همچنین ρ∞ چگالی جریان آزاد و C سرعت صدا است. نمودار ضریب فشار CP در اعداد ماخ مختلف در شکل ۹ نشان داده شده است. از آنجایی که فشار دینامیک برای تمام ساچمه‌ها در یک عدد ماخ مشخص ثابت باقی می‌ماند، هر تغییری در نمودار CP به علت تغییر فشار استاتیک خواهد بود. در نتیجه، کاهش ناگهانی CP در جلوی اولین ساچمه در مقایسه با موارد دیگر، یک اختلاف قابل توجه را بین P و P∞ در این ناحیه نشان می‌دهد، که مشخص می‌کند خطوط جریان به یکدیگر نزدیک می‌شوند و باعث رشد سرعت از نقطه سکون به مقدار ماکزیمم در لبه‌ها می‌شوند. دوباره، چنین گرادیان پرشیبی تأیید می‌کند که اولین ساچمه با موقعیتی روبرو می‌شود که در آن درگ فشاری بیشتر از موارد دیگر است. در نتیجه، شیب زیاد در جلوی یک پرتابه، درگ فشاری قابل توجهی را به وجود می‌آورد.

علاوه بر این، CP تا جلوی نقطه سکون دارای مقدار مثبت است، جایی که P بزرگتر از P∞ است، و باعث می‌شود جریان سیال در این ناحیه ساکن شود. برعکس، گرادیان فشار بعد از نقطه سکون معکوس می‌شود و سرعت جریان به نقطه مینیمم نمودار CP افزایش می‌یابد، جایی که جریان سرعت ماکزیمم خودش را تجربه می‌کند. می‌توان این حالت را همچنین در شکل ۱۰ مشاهده کرد که کانتور‌های عدد ماخ را در M∞ = 0.۷ اطراف اولین ساچمه نشان می‌دهد. در این عدد ماخ، نقطه مینیمم نمودار CP درست قبل از x = 0.4 mm رخ می‌دهد که با سرعت ماکزیمم جریان سیال منطبق است، همانطور که در شکل نشان داده شده است. به علاوه، شکل ۷ تغییر سرعت جریان را نیز نشان می‌دهد. همانطور که می‌توان مشاهده کرد، درست بعد از نقطه سکون فاصله بین خطوط جریان به طور قابل توجهی کاهش می‌یابد، که تحلیل‌های قبلی را ثابت می‌کند. برای توضیح بیشتر این مسئله، کانتور‌های زیادی اطراف ساچمه‌ها در M∞ = 1.۰ در شکل ۱۱ نشان داده شده است.

شکل ۹: ضرایب فشار در M∞ = 0.۷, ۱.۰, ۱.۳ برای (a) اولین ساچمه، (b) دومین ساچمه، و (c) سومین ساچمه.

 

شکل ۱۰: کانتور‌های عدد ماخ اطراف نقطه سرعت ماکزیمم در M∞ = 0.۷

 

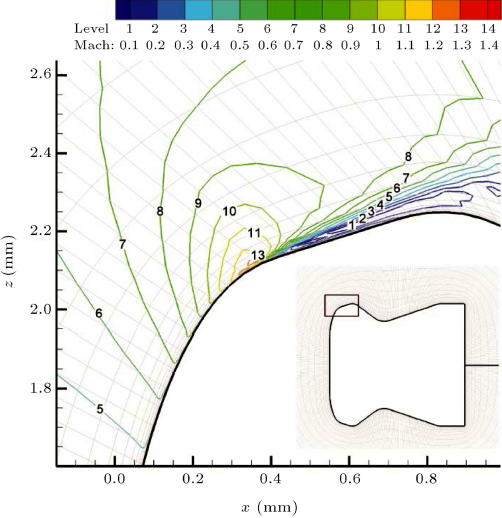
در نهایت، کانتور‌های فشار نشان داده شده در شکل ۱۲ بررسی شدند. ناحیه ویک، به صورت ناحیه کم فشار مستقر در پشت ساچمه، می‌تواند به طور واضح شناسایی شود. همانطور که مشخص است، سطح کانتور فشار مینیمم اطراف نقطه سرعت ماکزیمم رخ می‌دهد.

۸- نتایج دینامیک و بحث‌ها

در این بخش به منظور بررسی مسیر، کاهش ماخ، تغییرات تکانه، و زمانی که در آن پرتابه یک فاصله مشخص را طی می‌کند، حل سیستم معادلات دیفرانسیلی (معادلات (۵) و (۶)) به عنوان معادلات حاکم بر حرکت ساچمه‌ها برای ۲۵ متر اول مسیرشان مورد توجه قرار می‌گیرند.

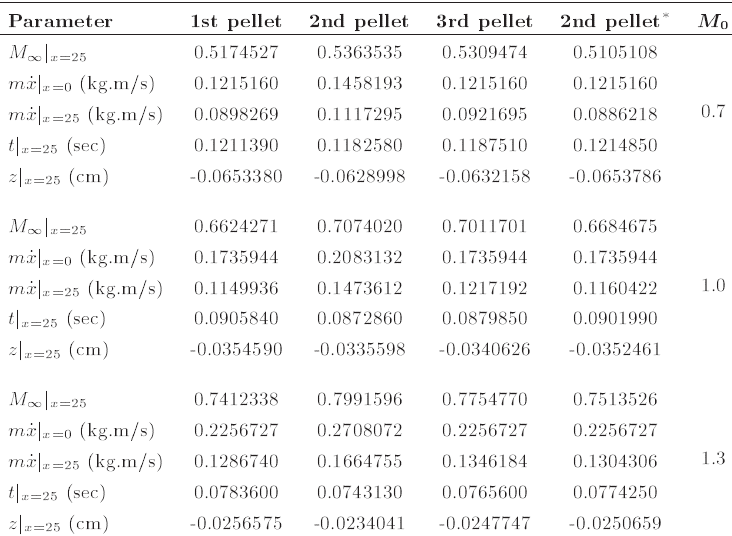
مسیر‌های اولین ساچمه در اعداد ماخ اولیه مختلف (M0) در شکل ۱۳ نشان داده شده است.

همانطور که انتظار می‌رود، انحراف مسیر از یک خط افقی، با افزایش M0 کاهش می‌یابد. در اینجا برای پوشش کل دامنه جریان تراصوتی، تغییر ارتفاع در سه عدد ماخ اولیه ۰.۷، ۱.۰ و ۱.۳ در نظر گرفته می‌شود. مقدار تغییر ارتفاع در M0 = 1.0 به عنوان یک مقدار مرجع در نظر گرفته می‌شود. همانطور که می‌توان مشاهده کرد، اختلاف بین مقدار مرجع و M0 = 0.7 بیشتر از اختلاف در مورد M0 = 1.3 است، و حاکی از آن است که تغییر ارتفاع در اعداد ماخ اولیه کمتر، برجسته‌تر خواهد بود.

به علاوه، افت سرعت اولین ساچمه در اعداد ماخ اولیه مختلف در ۲۵ متر اول مسیر، در شکل ۱۴ نشان داده شده است. همانطور که این نمودار نشان می‌دهد، در اعداد ماخ اولیه بیشتر، فاصله سریع‌تر پیموده می‌شود. شایان ذکر است که اختلاف بین سرعت‌های اولیه و نهایی ساچمه بسیار بیشتر از اعداد ماخ اولیه پایین‌تر هستند. جایی که تکانه نهایی ساچمه نقطه مورد توجه ما است، این نتیجه مهم است.

کاهش عدد ماخ تمام ساچمه‌ها در طول ۲۵ متر اول مسیرشان در شکل ۱۵ نشان داده شده است. اگرچه نمودار CD ساچمه‌ها نشان می‌دهد که سومین ساچمه دارای مقدار ضریب درگ مینیمم است، شکل ۱۵ آشکار می‌کند که مینیمم مقدار کاهش عدد ماخ به ساچمه دوم تعلق دارد. این تناقض آشکار به وسیله در نظر گرفتن جرم ساچمه‌ها حل می‌شود. همانطور که در جدول ۱ نشان داده شده است، ساچمه دوم سنگین‌تر از دیگر ساچمه‌ها است. برای دادن سرعت اولیه مشابه به دو پرتابه دیگر که دارای وزن‌های متفاوت هستند، ساچمه سنگین‌تر به تکانه بیشتری نیاز دارد. در حقیقت، تکانه اضافی باعث می‌شود پرتابه سنگین‌تر تغییر سرعت کمتری را تجربه کند.

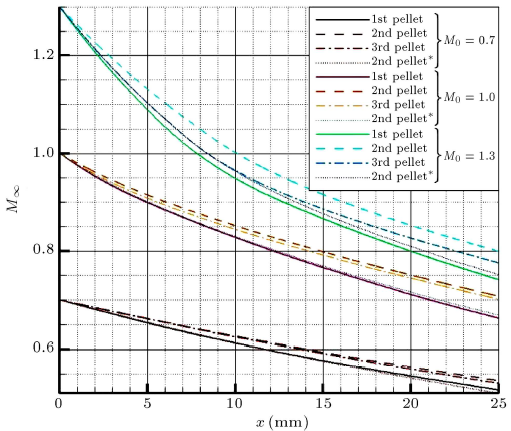
جدول ۲ چند پارامتر دینامیک را برای ساچمه‌ها در سه عدد ماخ مختلف مقایسه می‌کند. با نادیده گرفتن جمله (ż/ẋ)۲ مربوط به معادلات دینامیک حاکم (معادلات (۵) و (۶)) به دست می‌آوریم:

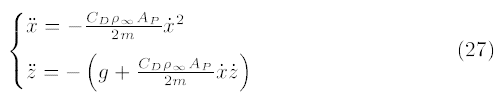
همانطور که مشخص است، ẍ و z̈ به طور معکوس با جرم پرتابه‌ها متناسب هستند. در نتیجه، اگر دومین ساچمه دارای وزن مشابهی با دیگر ساچمه‌ها بود، تغییر ارتفاع آن بیشتر از ساچمه سوم بود. در نتیجه، نتایج دینامیکی برای یک ساچمه خیالی از نوع دوم با جرم ۰.۵ g به وسیله علامت ستاره (*) در شکل ۱۵ و جدول ۲ نشان داده شده است، که تحلیل‌های آیرودینامیکی و دینامیکی فوق‌الذکر را تأیید می‌کند.

شکل ۱۱: کانتور‌های عدد ماخ در M∞ = 1.۰ اطراف (a) اولین ساچمه، (b) دومین ساچمه، و (c) سومین ساچمه.

 

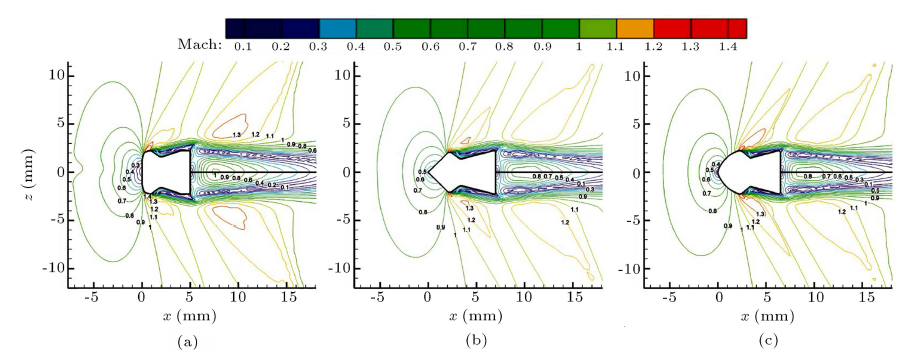
شکل ۱۲: کانتور‌های فشار در M∞ = 1.۰ اطراف: (a) اولین ساچمه، (b) دومین ساچمه، و (c) سومین ساچمه.

 

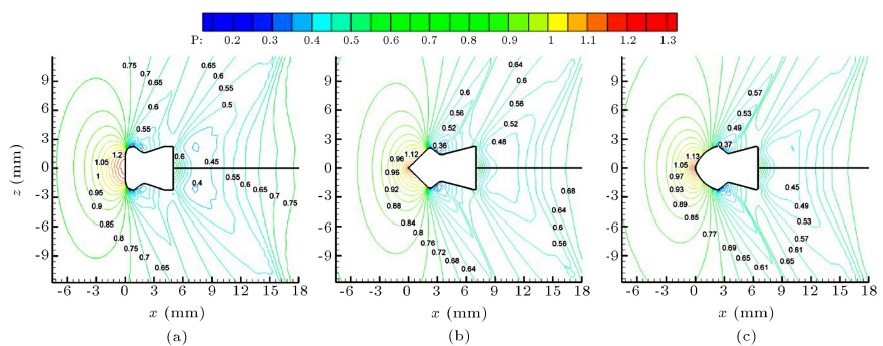
شکل ۱۳: مسیر اولین ساچمه در اعداد ماخ اولیه مختلف.

 

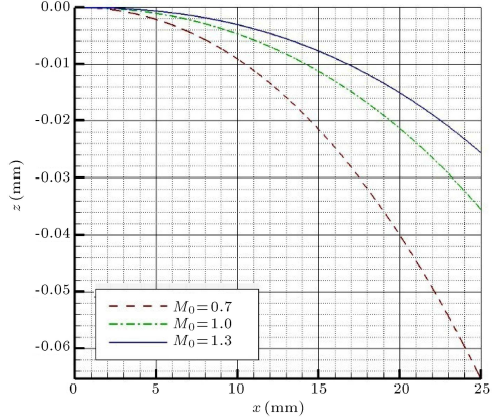
شکل ۱۴: افت سرعت با زمان در ۲۵ متر اول مسیر برای اولین ساچمه.

جدول ۲: نتایج دینامیکی برای ۲۵ متر اول مسیر.

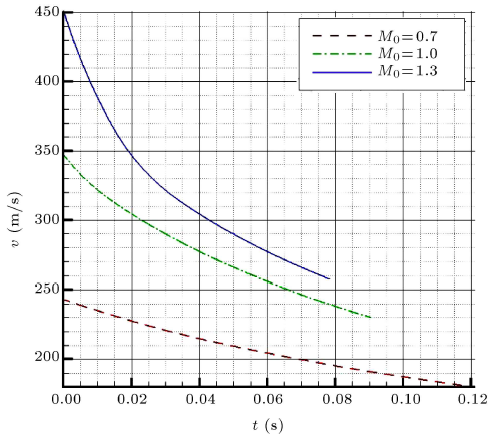
شکل ۱۵: کاهش عدد ماخ با زمان برای تمام ساچمه‌ها در ۲۵ متر اول مسیر

 

۹- نتیجه‌گیری‌ها

با استفاده از تحلیل آیرودینامیکی، ساچمه سرگرد (ساچمه سوم) در چند عدد ماخ بهترین رفتار آیرودینامیکی را نسبت به ساچمه‌های دیگر نشان داد؛ با این وجود، ساچمه دوم بهترین رفتار‌های دینامیکی را از نظر افت ارتفاع و تکانه نهایی نشان می‌دهد. علاوه بر این، سومین ساچمه بهترین نتایج دینامیکی را نسبت به اولین ساچمه نشان می‌دهد. همچنین، پرتابه بهتر بین اولین و دومین ساچمه بر اساس نتایج آیرودینامیکی و دینامیکی به دست آمده، پرتابه دوم است. از طرف دیگر، اگر دومین ساچمه دارای وزن مشابهی با ساچمه‌های دیگر بود (یعنی ساچمه دوم خیالی)، بر اساس جدول ۲، به ترتیب سومین، دومین و اولین ساچمه از نظر آیرودینامیکی و دینامیکی ترجیح داده می‌شدند.

زندگی‌نامه

مهدی رافعی مدرک لیسانسش را در سال ۲۰۰۶ در رشته مهندسی مکانیک از دانشگاه آزاد مشهد گرفت و مدرک فوق لیسانسش را در سال ۲۰۰۹ در رشته تبدیل انرژی از دانشگاه فردوسی مشهد گرفت. او قبلاً دو مقاله در کنفرانس‌های بین‌المللی منتشر کرده است. در حال حاضر او در دانشگاه New South Wales در سیدنی استرالیا دانشجوی دکترا است.

علی رضا تیمورتاش مدرک لیسانسش را در سال ۱۹۸۳ در رشته مهندسی مکانیک از دانشگاه فردوسی مشهد گرفت و مدرک فوق لیسانسش را در سال ۱۹۸۷ در رشته مهندسی مکانیک (ترمو سیالات) از دانشگاه صنعتی شریف در تهران گرفت، و مدرک دکترای خود را در سال ۲۰۰۲ در رشته تبدیل انرژی از دانشگاه فردوسی مشهد گرفت. او اکنون در دانشگاه فردوسی مشهد به عنوان دانشیار مشغول به کار است. او یک کتاب در رشته مکانیک سیالات، ۴۰ مقاله در کنفرانس‌های بین‌المللی، و ۲۸ مقاله علمی منتشر کرده است. او همچنین مسئول چندین پروژه کاربردی بوده است.