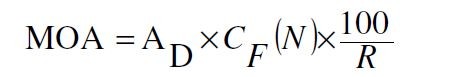تجزیه و تحلیل گروپ یا جمع تیر در تیراندازی
تجزیه و تحلیل گروپ یا جمع تیر در تیراندازی
آنالیز آماری اندازۀ گروپ
رابطۀ میان دقت ذاتی تفنگ و اندازۀ گروپی که میتواند در دامنۀ خاصی شلیک کند بسیار جالب است. مقالۀ حاضر این رابطه را به گونهای نشان میدهد که به وضوح دقت اسلحه را به اندازۀ گروپی که ایجاد میکند پیوند میدهد. جدولی نمایش داده شده است که به تیرانداز اجازه میدهد دقت واقعی اسلحه بر اساس دقیقۀ زاویه (MOA) را از یک یا چند گروپ تخمین بزند. فرضیۀ مهم در این بحث این است که ما با یک مدل آماری بسیار ساده روبرو هستیم که فاکتورهای متعارفی که سبب پراکندگی یک گروپ میشوند مانند تیرانداز، باد، ساچمه های نامتعادل و غیره را در نظر نمیگیرد. متداولترین روش برای تعیین اندازۀ گروپ یکی از روشهای بسیار متداول برای اندازهگیری دقت یک تفنگ، شلیک چندین تیر (گروپ) و اندازهگیری میانگین فاصلۀ پانچ دو شات با بیشترین فاصله از یکدیگر در هر گروپ است. فرض ما در اینجا این است که این کار در محدودۀ ۱۰۰ یاردی انجام میشود. سپس تیرانداز با استفاده از تقریب «اینچ 1MOA = 1 در ۱۰۰ یارد» ، این فاصله را به MOA تبدیل میکند. برای مثال، با توجه به هدف نشان داده شده در شکل ۱، برای ۳ شات در ۱۰۰ یاردی: روش متداول اندازهگیری گروپبرای یک هدف در فاصلۀ ۱۰۰ یاردی، فاصلۀ زاویهای MOA ۱ یا ۶۰/۱ درجه، بسیار نزدیک به ۱ اینچ است، اما دقیقاً ۱ اینچ نیست:
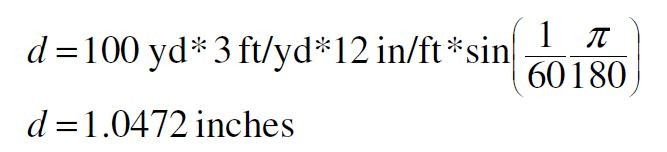
یکی دیگر از اندازهگیریهای متداول، Mil یا میلیرادیان یا یک هزارم رادیان است. PI*2 رادیان در ۳۶۰ درجه وجود دارد، بنابراین یک میلیرادیان برابر است با:
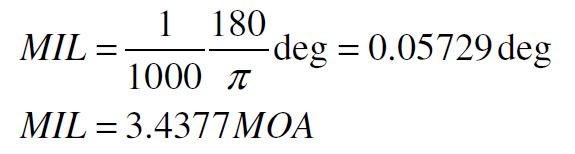
بنابراین مساوی پنداشتن فاصلۀ ۱ اینچ در ۱۰۰ یارد با MOA ۱ یک تقریب معتبر است. ما از این تقریب برای ادامۀ این مقاله استفاده خواهیم کرد. اگر خواننده تمایل به اندازهگیری بر حسب میلیرادیان داشته باشد، انجام تبدیلهای لازم به عهدۀ خواننده خواهد بود.
دقت و تکرارپذیری
اکثر تیراندازان به اندازۀ گروپ به عنوان شاخصی برای دقت تفنگ اشاره میکنند، در حالی که در حقیقت شاخصی برای تکرارپذیری تفنگ است.
تیرانداز یک گروپ را در یک نقطۀ هدف خاص (POA) شلیک میکند، و مرکز گروپ حاصل یا نقطۀ برخورد (POI) معمولاً تا حدودی از POI یا POA انحراف پیدا میکند. این انحراف نشان دهندۀ دقت تفنگ است، زیرا این خطا یا باید با استفاده از تنظیمات دوربین، یا با استفاده از یک گیرۀ در هنگام شلیک شات از بین برود. با فرض اینکه دوربین را میتوان به طور مناسب تنظیم کرد، یا تیرانداز میتواند دائماً POA را با اندازۀ لازم نگه دارد، این محتملترین POI برای هر شلیک خواهد بود. این دقت تحت تأثیر متغیرهای متعددی مانند وزن ساچمه ، میزان باد ، ثبات ساچمه و توازن وزنی آن، لولۀ تفنگ و باد و … قرار دارد. ما این تأثیرات را در ادامۀ مقاله نادیده میگیریم.
هنگامی که یک POI مشخص ایجاد میشود، یک گروپ به طور (معمولاً) تصادفی در اطراف میانگین POI توزیع میشود. اندازۀ این توزیع، تکرارپذیری تفنگ است. این همان چیزی است که در بالا به عنوان اندازۀ گروپ توصیف شده است. یک فرضیۀ مهم در اینجا این است که ما بسیاری از تأثیرات دنیای واقعی مانند تغییرات سرعت بین تیرها (که باعث پراکندگی عمودی میشود) و باد (که باعث پراکندگی افقی میشود و اندازه گروپ را میافزاید) و بسیاری دیگر را نادیده میگیریم.
یک تفنگ واقعاً دقیق دارای یک POI دقیق و تکرارپذیر و پراکندگی اندک پانچ تیر در اطراف آن نقطه است.
توزیع گاوسی (Gaussian) – یک مدل ساده از نحوۀ پراکندگی تیرها
فرضیۀ دیگری که ما در این مقاله داریم این است که پراکندگی تیرها در اطراف POI که در بالا ذکر شد، به سبک شناخته شدهای توزیع میشود. ما تصمیم گرفتیم از مدل توزیع نرمال یا گاوسی استفاده کنیم. این همان «منحنی زنگ – bell curve» مشهور است. بوضوح غیرممکن است تعیین کنیم که یک تفنگ یا تیرهای آن، یک توزیع نرمال حقیقی در اطراف POI خواهند داشت. اما از طریق مشاهدات بسیار نویسنده دریافته است که این مدل، توزیع گروپ بسیاری از تفنگها را نسبتاً دقیق توصیف میکند.
شکل ۲: توزیع گاوسی (نرمال) احتمال
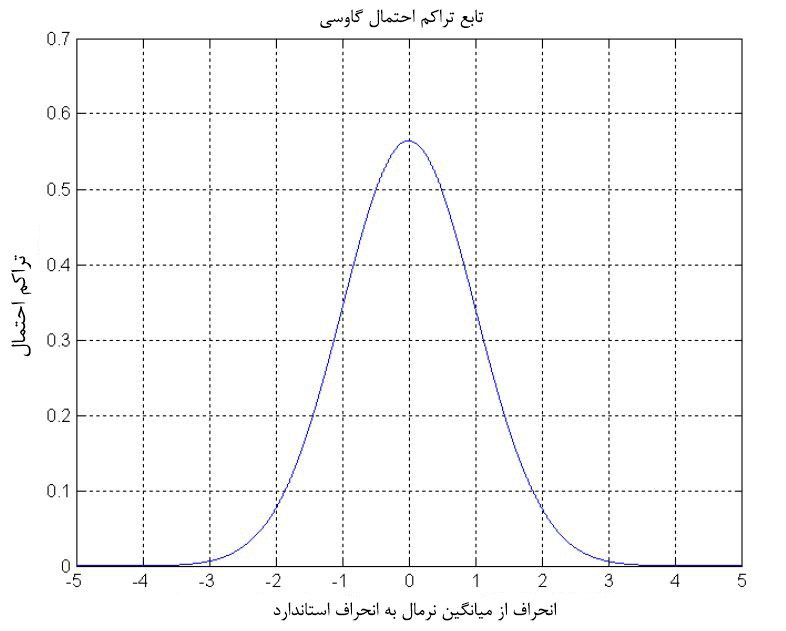
شکل ۲ توزیع دو طرفۀ گاوسی را به عنوان تراکم احتمال نشان میدهد. محور X انحراف از میانگین در واحد انحراف استاندارد است. انحراف استاندارد، یک انحراف خاص از میانگین (در این مورد میانگین صفر) را تعریف میکند که در درصد معینی از زمان انتظار میرود. این بدان معناست که اگر فرآیندی دارای این توزیع باشد، ۶۸.۲٪ از مواقع این مقدار بین ۱- و ۱+، ۹۵.۵٪ از مواقع بین ۲- و ۲+ و ۹۹.۷٪ از مواقع بین ۳- و ۳+ قرار میگیرد.
با این تعریف دقت در مدل بالا می توانیم برای پرتابه مورد تست خود انحراف استاندارد از مسیر پرواز واقعی را بصورت زاویه در MOA محاسبه کنیم .
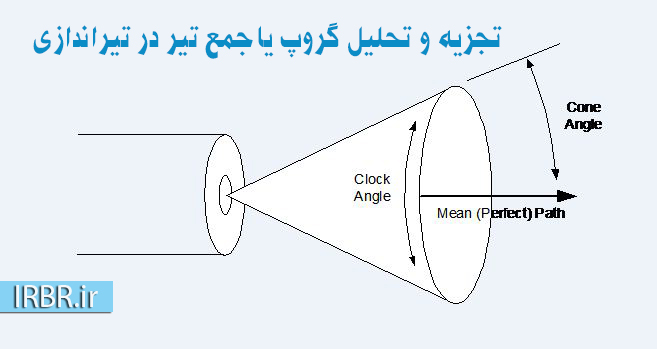
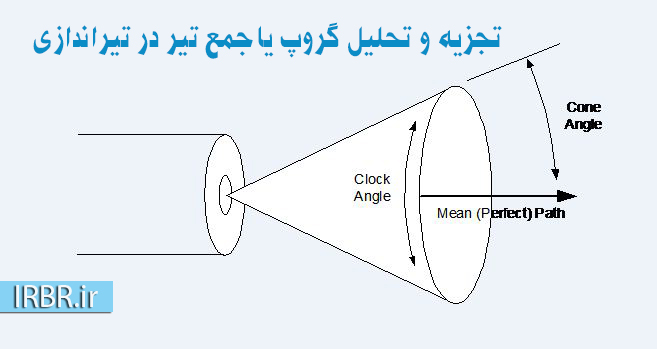
شکل ۳: زاویۀ انحراف شات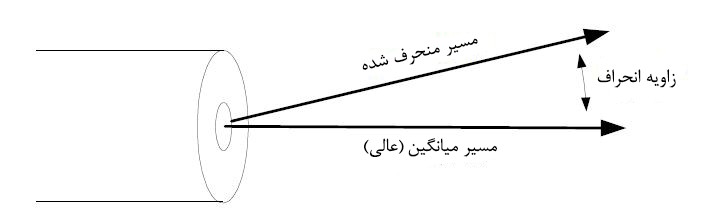 شکل ۳ زاویۀ انحراف را به شکل انحراف از مسیر مستقیم نشان میدهد. ما امیدوار هستیم مدل خود را به گونهای تعریف کنیم که این زاویۀ انحراف (زاویۀ مخروطی) دارای توزیع نشان داده شده در شکل ۲ باشد و هر شات با یک زاویۀ تصادفی با احتمال برابر در مسیر عالی (زاویۀ ساعت) خارج شود. شکل ۴ این تعریف را نشان میدهد.
شکل ۴: تعریف زاویۀ مخروط و زاویۀ ساعت
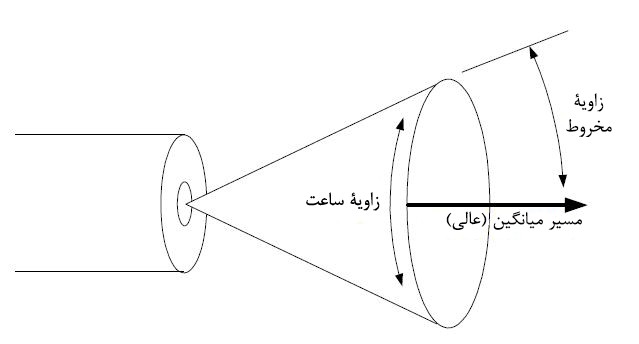
شکل ۳ زاویۀ انحراف را به شکل انحراف از مسیر مستقیم نشان میدهد. ما امیدوار هستیم مدل خود را به گونهای تعریف کنیم که این زاویۀ انحراف (زاویۀ مخروطی) دارای توزیع نشان داده شده در شکل ۲ باشد و هر شات با یک زاویۀ تصادفی با احتمال برابر در مسیر عالی (زاویۀ ساعت) خارج شود. شکل ۴ این تعریف را نشان میدهد.
شکل ۴: تعریف زاویۀ مخروط و زاویۀ ساعت
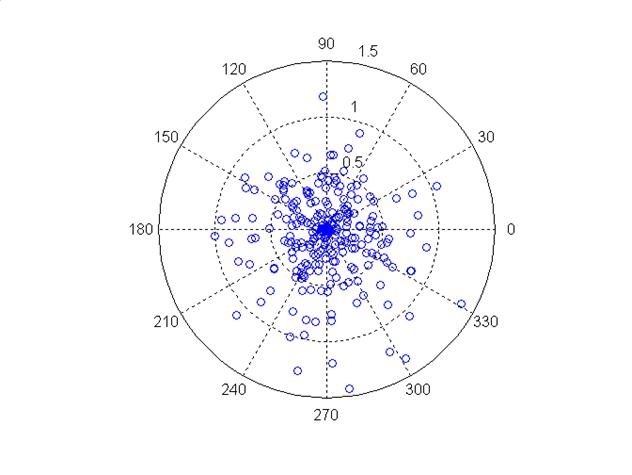
شکل ۵: هدف شبیهسازی شده پس از ۲۵۰ شات
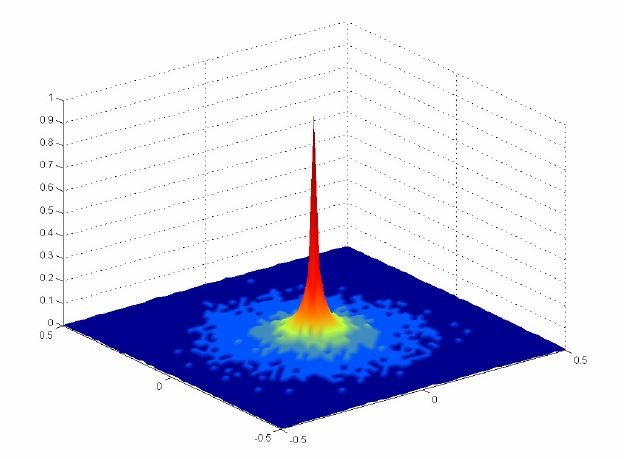
شکل ۶: توزیع POI هدف برای ۱۰۰۰۰۰ شات
|
تعداد شلیک |
Correction Factor |
|
۲ |
۱.۱۵۹ |
|
۳ |
۱.۱۵۸ |
|
۴ |
۰.۹۷۹ |
|
۵ |
۰.۸۷۶ |
|
۶ |
۰.۸۰۸ |
|
۷ |
۰.۷۵۹ |
|
۸ |
۰.۷۲۰ |
|
۹ |
۰.۶۹۳ |
|
۱۰ |
۰.۶۶۷ |
|
۱۱ |
۰.۶۴۶ |
|
۱۲ |
۰.۶۳۰ |
|
۱۳ |
۰.۶۱۴ |
|
۱۴ |
۰.۶۰۲ |
|
۱۵ |
۰.۵۹۰ |
|
۱۶ |
۰.۵۷۹ |
|
۱۷ |
۰.۵۷۱ |
|
۱۸ |
۰.۵۶۲ |
|
۱۹ |
۰.۵۵۴ |
|
۲۰ |
۰.۵۴۶ |