تفنگ بادی – فیزیک
تفنگ بادی – فیزیک
مقدمه ای بر تفنگ بادی از منظر فیزیک – بخش ۱
بخش اول: آیزاک نیوتن و تفنگ بادی نوشته‌ی مایک رایت (Mike Wright)
می‌توان گفت مقاله‌ی حاضر به دنبال درخواست‌های مطرح شده در نمایشگاه تیراندازی بریتانیا در نیوارک منتشر شده است. من و جیم یک روز را در آن‌جا گذراندیم و با تعدادی از خوانندگان مجله صحبت کردیم. بیش‌تر آنان نظری یکسان داشتند: آن‌ها به بخش فنی مجله بسیار علاقه‌مند بودند، اما از قسمت‌هایی از مقاله‌ها سر در نمی‌آوردند. چرا مطلبی به زبان ساده نمی‌نوشتیم که مفاهیم علمی پایه‌ای که مبنای نوشته‌های ما تشکیل می‌دهند را توضیح دهد؟ انصافا، مدتی بود که جیم همین پیشنهاد را مطرح می‌کرد، اما من فکر می‌کردم بهتر است بخشی از کتابی باشد که در حال کارکردن بر روی آن هستیم. مشکل این‌جاست که کتاب هنوز تمام نشده است. بنابراین، به دنبال درخواست خوانندگان، در این‌جا بخش اول از دو مقاله درباره‌ی مفاهیم پایه‌ی فیزیکی در تفنگ بادی ارائه می‌شود.
گالیله و نیوتن
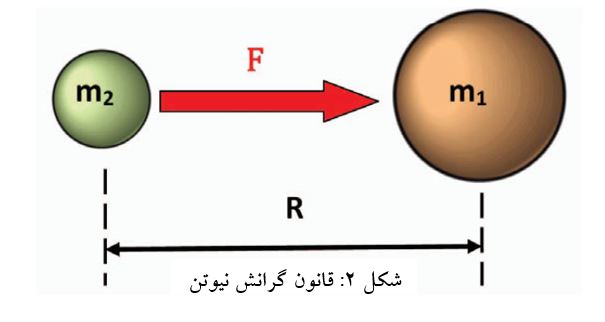
در دنیای غرب، می‌توان ردپای پیدایش فیزیک کلاسیک را تا دوران رنسانس، در فاصله‌ی قرون ۱۴ تا ۱۷ میلادی، دنبال کرد. به منظور درک نحوه‌ی حرکت ماه، ستارگان و سیارات، دانشمندانی هم‌چون کوپرنیک، کپلر و گالیله (متولد سال ۱۵۶۴) به تدریج ایده‌هایی جدید در رابطه با قوانین حرکت اجرام آسمانی مطرح نمودند. اما به چالش کشیدن ایده‌های حاکم هیچ‌گاه خالی از دردسر نبوده است. گالیله توسط دادگاه تفتیش عقاید روم ، که او را به دلیل اظهاراتش درباره‌ی مرکزیت خورشید – و نه زمین – در منظومه‌ی شمسی مرتد می‌دانست ، محاکمه گردید. وی در ادامه ناچار شد دهه‌ی بعدی زندگی خود را تا زمان مرگش در سال ۱۶۴۲ در حبس خانگی بگذراند. با وجود این، بالاخره در سال ۱۶۳۸ کتاب وی با عنوان «گفتارهایی درباره‌ی دو علم جدید»، که به ایده‌های گالیله در رابطه با قوانین حرکت و اصول مکانیک می‌پرداخت، منتشر شد. مطالب این کتاب، یکی از سنگ‌بناهای کار آیزاک نیوتن – که می‌توان او را در کنار گالیله به عنوان پدران فیزیک کلاسیک شناخت- را تشکیل می‌داد.
در یک تقارن زمانی عجیب آیزاک نیوتن (۱۷۲۷-۱۶۴۲) در روز کریسمس همان سالی به دنیا می‌آید که گالیله از دنیا می‌رود و تقریبا نیم قرن بعد «اصول ریاضی» را منتشر می‌کند. این کتاب بر مبنای کارهای گالیله و دیگران شکل گرفته بود و از شاخه‌ای جدید در ریاضیات (حساب دیفرانسیل و انتگرال) استفاده می‌کرد تا قوانین مکانیک را در قالب مجموعه قوانینی ساده که امروزه با عنوان قوانین نیوتن شناخته می‌شوند، تدوین نماید. خوب، این قوانین چه هستند و چگونه می‌توانیم آن‌ها را به کار بگیریم؟
اینرسی و جاذبه
قانون اول نیوتن یا «قانون اینرسی» بیان می‌کند که «جسم ساکن، ساکن باقی می‌ماند و جسم متحرک به حرکت خود با سرعت ثابت و در همان جهت ادامه می‌دهد، مگر آن‌که نیرویی خارجی به آن‌ها اعمال شود.» این عبارت به ظاهر بدیهی، پیچیده‌تر از آن است که به نظر می‌رسد و ایده‌ی اینرسی را مطرح می‌کند. اینرسی ویژگی مشترک همه‌ی اجسامی است که در برابر تغییر وضعیت از خود مقاومت نشان می‌دهند. به قول ریچارد فیمن «اشیاء به کار خود ادامه می‌دهند، مگر آن‌که به انجام کار دیگری وادار شوند». برای مثال، توقف ناگهانی خودرو خود را تصور کنید: بدن شما به دلیل اینرسی، مایل است وضعیت حرکت رو به جلوی خود را حفظ کند. بنابراین شما به حرکت رو به جلوی خود به سمت داشبورد ماشین که اکنون ساکن است ادامه می‌دهید، مگر آن‌که کمربندی ایمنی جلوی شما را بگیرد. همین اصل در هنگام بیرون آوردن آخرین قطره‌ی سس از داخل بطری حاکم است: بطری را با سرعت جلو آورده و ناگهان متوقف می‌کنید، به این امید که سس به حرکت روی به جلوی خود به سمت بشقاب شما ادامه دهد.
نیوتن دریافت که اجسامی که بر زمین می‌افتند نیز باید تحت تاثیر نیرویی باشند که آن‌ها را به حرکت وا می‌دارد. بنا بر روایتی ساختگی، این موضوع هنگام دیدن افتادن سیبی از درخت به وی الهام شد. به هر حال حتی اگر این طور باشد، فراست فوق‌العاده‌ی نیوتن در درک مفهوم میدان نیرویی است که سیب را به سمت زمین جذب می‌کند.
شکل ۱ ایده‌ی انتشار میدان نیروی کششی توسط جرمی کروی را نشان می‌دهد. شدت میدان با افزایش فاصله تا منبع کاهش می‌یابد. از آن‌جا که جرم کروی در نظر گرفته شده است، شدت [نیرو] متناسب با معکوس توان دوم فاصله کاهش می‌یابد. چنین رابطه‌ای «قانون مربع معکوس» خوانده می‌شود. شکل ۲ نشان می‌دهد که چگونه دو جرم در اثر میدان گرانش یکدیگر را جذب می‌کنند. معادله‌ی نیروی جاذبه با عنوان «قانون گرانش عمومی نیوتن» شناخته می‌شود. «G» ثابت گرانش بوده و فرض شده است که مقدار آن در همه جا ثابت و معتبر است. مقدار G در سیستم SI (متریک) برابر با ۶.۶۷۳۸×۱۰-۱۱ اندازه‌گیری شده است.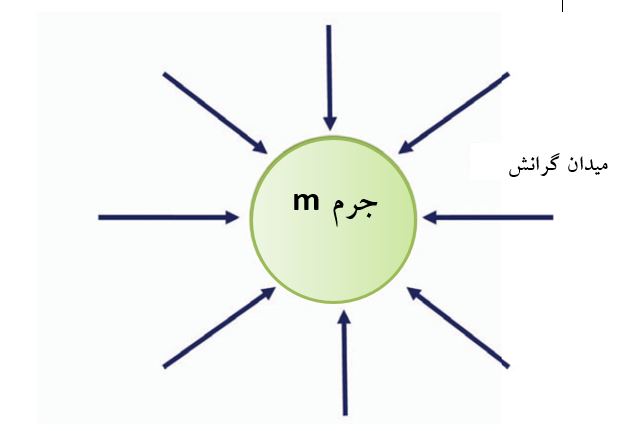
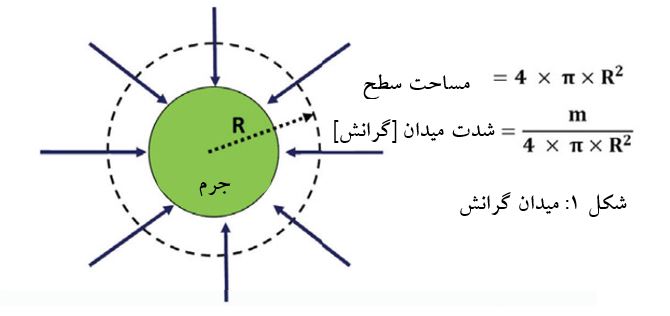
برای درک بهتر این قانون، اجازه دهید نیروی وارد بر جسمی به جرم ۱ کیلوگرم در سطح زمین را محاسبه کنیم. میانگین شعاع زمین ۶۳۷۵ km و وزن تخمینی آن ۵.۹۷۲۲ × ۱۰۲۴ kg (5.9722 تریلیون، تریلیون کیلوگرم) است. بنابراین نیروی وارد بر جرم m کیلوگرم برابر است با:
این نیرو همان وزن جسم مورد نظر بوده و برای جسمی به جرم ۱ کیلوگرم در سطح زمین برابر با ۹.۸۱ نیوتن است. بنابراین نتیجه می‌گیریم که وزن هر جرم در سطح زمین برابر با حاصل‌ضرب جرم آن بر حسب کیلوگرم در ۹.۸۱ است (برای مثال، وزن جرمی ۵ کیلوگرمی کمی بیش از ۴۹ نیوتن است). البته این رابطه خارج از زمین صدق نمی‌کند: جرم ماه ۱.۲ % جرم زمین و شعاع آن ۲۷% شعاع زمین است. برابر این وزن جسمی به جرم ۱ کیلوگرم در سطح ماه تنها ۱.۶۳ نیوتن خواهد بود. اما نگران نباشید، اگر یک کیلو سیب‌زمینی با خود به ماه ببرید، آن‌جا هم همان تعداد سیب‌زمینی خواهید داشت، که البته سبک‌تر به نظر خواهند رسید 
.
نیرو، جرم و شتاب
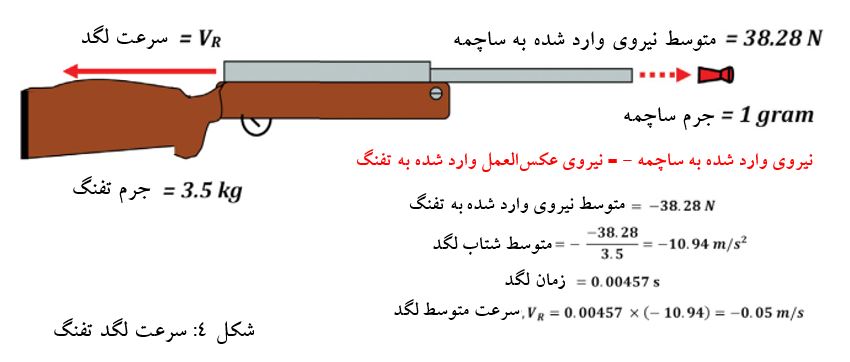
نیوتن می‌دانست که آزمایش‌های گالیله نشان داده‌اند که همه‌ی اجسام از ارتفاعی مشخص با سرعت یکسانی به سمت زمین سقوط می‌کنند. این بدین معناست که سیب و گلوله‌ی توپی که به طور هم‌زمان از یک پنجره در ساختمانی بلند رها می‌شوند، دقیقا در یک زمان به زمین برخورد می‌کنند. این امر حاکی از آن است که میدان جاذبه به سیب و گلوله‌ی توپِ ساکن، شتاب یکسانی می‌دهد. اما گلوله توپ بسیار سنگین‌تر از سیب است و قطعا با نیروی بسیار بیش‌تری به زمین برخورد می‌کند. بنا بر نظریه‌ی گرانش این نیرو باید با جرم جسم در حال سقوط نسبت مستقیم داشته باشد. نیوتن این دو موضوع را در آن‌چه که امروزه «قانون دوم نیوتن» خوانده می‌شود، خلاصه کرده است:
با توجه به بخش قبل، ظاهرا شتاب ناشی از جاذبه در جسم در حال سقوط برابر با ۹.۸۱ m/s2 است. اما قانون شتاب برای هر جرمی که نیرویی به آن وارد شود صدق می‌کند. برای مثال، می‌توان از آن برای تخمین نیروی پیش‌راننده‌ی مورد نیاز برای شلیک موشک به فضا یا قدرت ترمز مورد نیاز برای متوقف کردن اتومبیل، یا حتی فشار مورد نیاز برای رساندن ساچمه به سرعت لازم در تفنگ بادی استفاده کرد. در واقع، ما در ادامه‌ی این مقاله بر توضیح قوانین نیوتن از طریق اعمال آن‌ها در تفنگ بادی PCP تمرکز می‌کنیم. به منظور ساده‌تر شدن مسئله، ما اصطکاک و سایر عوامل خارجی را نادیده می‌گیریم.
شکل ۳ ساچمه‌ای را نشان می‌دهد که از دهانه‌ی لوله‌ی یک PCP به جلو رانده می‌شود. فرض کنید که ساچمه‌ی ۵.۵ میلی‌متری (۰.۲۲) جرمی برابر یک گرم داشته باشد (در حدود ۱۵.۴ دانه[۲]) و …
اشتراک گذاری
