بالستیک داخلی در تفنگ بادی

بالستیک داخلی تفنگ بادی

پرتابه‌شناسی[۱] داخلی سلاح گرم یا سلاح توپخانه حرکت ساچمه، گلوله یا پوکه را در داخل لوله بررسی می‌کند. در کل، محاسبه سرعت مازل سلاح گرم باروتی از روی اصول اولیه دشوار است، زیرا احتراق باروت سریع است و دمای گاز (حاصل از اشتعال یا سوزش باروت) را خیلی سریع بالا می‌برد، که تحلیل را فوق‌العاده پیچیده می‌کند. تفنگ‌های بادی مورد ساده‌ای هستند که می‌توانیم برای آنها برآوردهای معقولی داشته باشیم. در این برآوردها، امکان محاسبه سرعت گریز وجود دارد. شاید تعجب‌برانگیز باشد که سرعت گریز به طول لوله بستگی دارد (توپچی‌ها صدها سال بر سر این موضوع بحث داشتند، تا اینکه از طریق آزمایش و بعدها به‌صورت نظری مشخص شد). در اینجا، می‌بینیم که تحلیل فیزیکی ساده، که در توان دانش‌آموزان دبیرستان یا دانشجویان سال اول فیزیک دوره لیسانس هم هست، نه‌تنها سرعت گریز را به دست می‌آورد، بلکه چگونگی وابستگی آن را هم به طول لوله نشان می‌دهد.

این تحلیل برای تفنگ‌های بادی ساده‌تر است، زیرا به طور منطقی می‌توانیم فرض کنیم که دما در فاز انبساط گاز ثابت است، بنابراین، به‌جای قانون گاز پیچیده‌تر وابسته به دما، قانون بویل در اینجا حاکم است. ماشه گاز فشرده را آزاد می‌کند؛ فشار این گاز ساچمه را از لوله تفنگ به بیرون پرتاب می‌کند. می‌توانیم از تأثیر نیروی پسای آئرودینامیک در لوله صرف‌نظر کنیم، ولی باید اصطکاک تماسی بین ساچمه و لوله را لحاظ کنیم. در اینجا، فرض می‌شود که نیروی اصطکاک ثابت است (مستقل از سرعت ساچمه). شاید این برای ساچمه‌های سربی دامنه‌دار (دیابولو) [۲] واقع‌گرایانه نباشد: طراحی این ساچمه‌ها طوری است که فشار گاز ته ساچمه را منبسط می‌کند تا روزنه بسته شود، تا در حین خروج گاز از شکاف بین ساچمه و لوله، قدرت به هدر نرود. شاید نیروی عادی بین ساچمه و لوله به فشار گاز بستگی داشته باشد. سه فرض دیگر وجود دارند: درزبندی بی‌نقص است، انرژی مصرفی برای چرخش ساچمه در حین حرکت در لوله تفنگ قابل‌چشم‌پوشی است و انرژی مصرفی برای شتاب گاز نیز قابل‌چشم‌پوشی است. همه مفروضات آخر منطقی هستند، ولی فرض بر اصطکاک ثابت نامطمئن است و فرض بر انبساط هم‌دمایی نیز خیلی نامطمئن است. بنابراین، انتظار می‌رود که پیش‌بینی مدل ساده ما تقریبی باشد. ساده‌سازی‌های مفروضات ما بدین معنی است که می‌توانیم عبارت تحلیلی را از مدل ساده‌مان برای سرعت گریز به دست آوریم.

سرعت مازل (ابتدای خروج از لوله) و طول لوله

چند نوع تفنگ بادی وجود ندارند که از لحاظ فشرده‌سازی هوا با هم متفاوت‌اند. تحلیل سازوکار تفنگ‌های بادی پیستون فنری پیچیده است و بنابراین، بیشتر آنها را بررسی نخواهیم کرد.

شکل ۱. تصویر تفنگ بادی. طول لوله L و سطح مقطع عرضی A = π(c/2)^۲, است که در آن، c کالیبر است. حجم مخزن گاز پیش از کشیدن ماشه v_۰ است. وزن ساچمه m است.

 در تفنگ‌های بادی، هوا از طریق اهرم چخماق کشی فشرده می‌شود؛ تفنگ‌های پی سی پی با اهرم چخماق کشی بکار می‌کنند و هوای فشرده را مستقیماً از سیلندر بیرونی مانند کپسول غواص‌ها دریافت می‌کنند؛ تفنگ‌های دی‌اکسیدکربن از محفظه پاورلت کوچک حاوی CO_۲ استفاده می‌کنند. این سه نوع تفنگ آخری، مخزنی را با هوای تحت‌فشار پر می‌کنند (از ۷۰۰ – ۲۰۰ atm). در اینجا، این سیستم را تحلیل می‌کنیم. در شکل ۱، می‌توانید مخزن هوای فشرده را ببینید (حجم V_۰ و فشار P_۰). با کشیدن ماشه، این گاز وارد لوله (سطح مقطع عرضی A و طول L) می‌شود و ساچمه را به بیرون هل می‌دهد (وزن m). فرض می‌کنیم که دمای گاز در این فاز انبساط خیلی تغییر نمی‌کند، بنابراین قانون بویل حکم می‌کند:

در اینجا، P(t) و V(t) به ترتیب فشار و حجم گاز در زمان t پس از کشیدن ماشه هستند، درحالی‌که P(0) = P_۰، غیره. طبق شکل ۱، می‌بینیم که

در اینجا، x(t) موقعیت ساچمه در لوله است (۰≤x≤L). در شکل ۱، ساچمه در موقعیت اولیه قرار دارد، بنابراین x(0) = 0. بنابراین، نیروی وارده بر ساچمه برابر است با

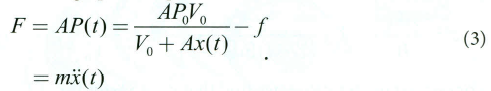
در معادله ۳، از نشانه گذاری نقطه نیوتن برای مشتق زمان استفاده می‌کنیم؛ f نیروی اصطکاک ثابت بین لوله و ساچمه است. این معادله تفکیک پذیر است، زیرا                    

و ادغام آن ساده است:  

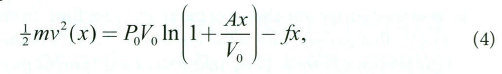
در اینجا،  است. توجه کنید که اولین عبارت سمت راست انرژی (W) آزادشده در اثر انبساط گاز از حجم اولیه به موقعیت x در لوله است و عبارت دوم اتلاف انرژی اصطکاک بین ساچمه و لوله است. عبارت سمت چپ انرژی (جنبشی) ساچمه است. برای تحلیل ساده شده ما، هیچ اتلاف انرژی در گرمایش گاز وجود ندارد.

سرعت گریز ساچمه برابر است با:

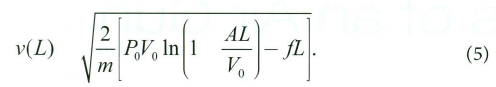
سرعت گریز معادله ۵ به‌ازای طول لوله در معادله زیر به اوج می‌رسد

که به‌سادگی مشخص است. فرض می‌کنیم که تولیدکننده تفنگ بادی ما پارامترهایی را انتخاب کرده تا معادله ۶ صدق کند و سرعت گریز به اوج خود برسد. با جای‌گذاری معادله ۶ در معادله ۵، داریم که

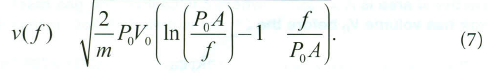
معادله‌های ۶ و ۷ در شکل‌های ۲.الف و ۲.ب رسم شده‌اند. شکل ۲.ج نشان می‌دهد که حذف f و v(L_max) چه نتیجه‌ای دارد. بنابراین، سرعت گریز را با توجه به طول لوله این نوع تفنگ به دست می‌آوریم. می‌بینیم که با افزایش طول لوله، سرعت گریز بالا می‌رود و سرعت افزایش برای لوله‌های بلندتر کمی آهسته می‌شود؛ این رفتار در سلاح‌های باروتی نیز دیده می‌شود، البته کاهش شتاب چشمگیرتر است.

برای گراف‌های رسم شده در شکل ۲، از این مقادیر برای پارامترها استفاده کرده‌ایم: P_۰ = 200 atm (2×۱۰^۷ Nm^-۲)؛ V_۰ = 16 cc (1.6 × ۱۰^-۵ m^۲) که در پاورلت CO_۲ عادی است؛ A = 1.6 × ۱۰^-۵ m^۲ برای تفنگ کالیبر ۱۷۷. و A = 2.5 × ۱۰^-۵ m^۲ برای تفنگ کالیبر .۲۲؛

 (۵.۲ × ۱۰^-۴ kg)  گرین m = 8  برای ساچمه .۱۷۷ و (۱.۰ × ۱۰^-۳ kg)  گرین m = 15 برای ساچمه ۲۲. . همچنین، در شکل ۲ توجه کنید که طول لوله را به حداقل ۱۵ سانتی‌متر (تپانچه بادی) و حداکثر ۵۰ سانتی‌متر (تفنگ بادی) محدود کرده‌ایم. تمام این ارقام جهت مثال هستند و منجر به سرعت گریز واقع‌گرایانه می‌شوند.

بازدهی  تفنگ بادی ما برابر نسبت انرژی ساچمه به انرژی گاز در سر لوله است که در قسمت زیر مشخص است:

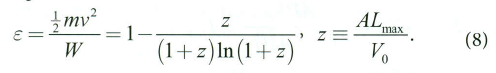
با آن مقدار پارامترها، می‌بینیم که  برای تفنگ ۱۷۷. و  برای تفنگ ۲۲. است: بیشتر انرژی برای غلبه بر اصکاک صرف شده است. چرا وقتی سرعت گریز بهینه‌سازی شده است، این قدر بازده آن پایین است؟ طول بیشتر لوله بدین معنی است که انرژی بیشتری صرف اصطکاک می‌شود، ولی لوله کوچکتر بدین معنی است که فشار گاز بیشتری هدر می‌رود؛ به ازای پارامترهای انتخابی مان، ]طبق معادلات ۱ تا ۳[ می‌بینیم که فشار گاز در سر لوله P(L) برابر ۷۱% فشار گاز اولیه P_۰ تفنگ ۱۷۷. است (۵۶% برای تفنگ ۲۲.). با خروج ساچمه از لوله، فشار گاز باقیمانده در هوا تلف می‌شود. بنابراین، برای به دست آوردن طول بهینه لوله، باید موازنه پایاپایی بین اصطکاک و اتلاف فشار هوا باشد.

طبق شکل‌های ۲.الف و ۲.ب توجه کنید که برای لوله‌های فوق‌العاده بلند، مدل ساده ما سرعت گریز فوق‌العاده بالایی را پیش‌بینی می‌کند. (انتظار داریم که حد بالایی سرعت گریز برای هر شلیک تفنگ بادی برابر سرعت صوت در هوا باشد، زیرا این سرعت امواج فشار است).

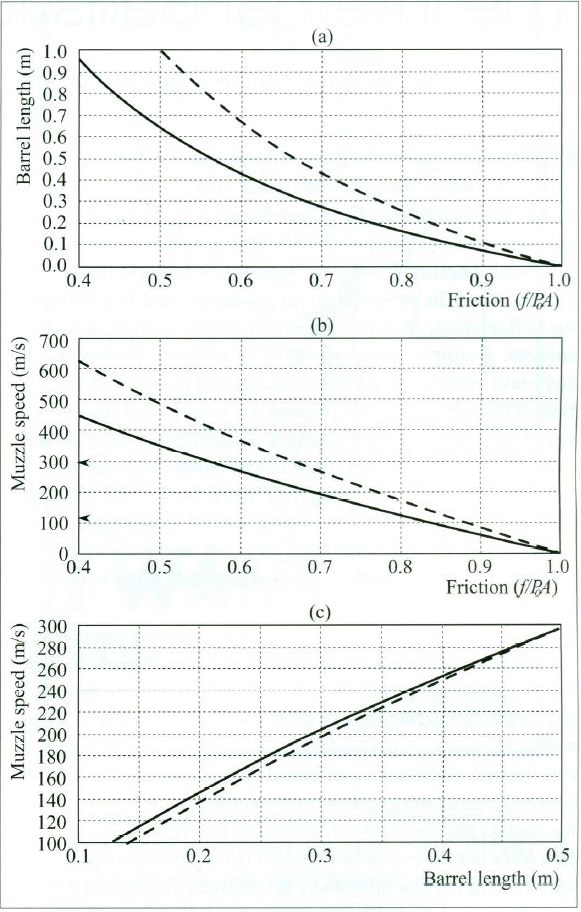
شکل ۲.الف. مقایسه طول لوله تفنگ بادی و اصطکاک بی بعد برای سرعت گریز بهینه. نمودارها برای تفنگ کالیبر ۲۲. (خط پررنگ) و تفنگ کالیبر ۱۷۷. (خط‌چین) هستند. ب. مقایسه سرعت گریز و اصطکاک بی بعد.  ج. مقایسه سرعت گریز و طول لوله برای بخش کوچکی از الف و ب که محدود به مقادیر واقعی طول لوله (تقریباً ۰.۱۵ متر تا ۰.۵ متر) هستند.

در این قسمت، فرض ما از انبساط هم‌دمایی خراب می‌شود. اگر انبساط موجب تغییر دمای گاز شود، می‌توانیم تغییر را برای انبساط کوچک در نظر نگیریم (طول پایین لوله)، ولی نه برای انبساط بزرگ. بنابراین، مدل ساده ما برای لوله‌های دراز با مشکل مواجه می‌شود.

خلاصه

این تمرین کوتاه نشان می‌دهد که سرعت گریز تفنگ هوایی همسو با طول لوله افزایش می‌یابد و مقادیر واقع‌گرایانه ما را برای سرعت گریز (در ازای پارامترهای ورودی واقع‌گرایانه) پیش‌بینی می‌کند. مقادیر غیرواقعی برای شرایطی به دست می‌آیند که فرض انبساط هم‌دمایی صدق نکند. (دانشجویان علاقه‌مند می‌توانند با تکرار تحلیل ما، به‌جای انبساط هم‌دمایی، انبساط بی‌دررو گاز کامل را فرض کنند. این تمرین عبارت متفاوتی را برای سرعت گریز ارائه می‌کند که به طول لوله بستگی دارد). این محاسبات شامل مفاهیم و روش‌های فیزیکی پایه‌ای ولی مهم می‌شود، از جمله انرژی مکانیکی و ترمودینامیک، اصطکاک تماس، نیرو، معادلات دیفرانسیل مقدماتی و بهینه‌سازی. به‌کارگیری این روش‌ها برای مسئله عملی نشانگر کاربرد آنهاست و احتمالاً برای دانشجویان از مثال ساده کتابی خشک جذاب‌تر است.

تقدیر و تشکر

نویسنده از دو داور بی‌نام کمال تشکر را دارد؛ توصیه‌های مفید و سازنده آنها این مقاله را بهبود بخشیده است.

[۱] Ballistics

[۲] Diabolo